
【题目】在一条笔直的公路上,A、B两地相距300千米.甲乙两车分别从A、B两地同时出发,已知甲车速度为100千米/小时,乙车速度为60千米/小时.经过一段时间后,两车相距100千米,求两车的行驶时间?
【答案】![]() 小时或
小时或![]() 小时或5小时或10小时.
小时或5小时或10小时.
【解析】
设当两车相距100千米时,两车行驶的时间为x小时,根据路程=速度×时间结合两车相距100千米即可得出关于x的一元一次方程,解之即可得出结论,注意分类讨论.
解:设当两车相距100千米时,两车行驶的时间为x小时,
根据题意得:
若两车相向而行且甲车离A地更近,则(100+60)x=300-100,
解得:x=![]() ;
;
若两车相向而行且甲车离B地更近,则(100+60)x=300+100,
解得:x=![]() ;
;
若两车同向而行且甲车未追上乙车时,则(100-60)x=300-100,
解得:x=5;
若两车同向而行且甲车超过乙车时,则(100-60)x=300+100,
解得:x=10;
∴两车的行驶时间为![]() 小时或
小时或![]() 小时或5小时或10小时.
小时或5小时或10小时.


科目:初中数学 来源: 题型:
【题目】某班“2016年联欢会”中,有一个摸奖游戏:有4张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,2张是哭脸,现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.
(1)现在小芳和小霞分别有一次翻牌机会,若正面是笑脸,则小芳获奖;若正面是哭脸,则小霞获奖,她们获奖的机会相同吗?判断并说明理由.
(2)如果小芳、小明都有翻两张牌的机会.翻牌规则:小芳先翻一张,放回后再翻一张;小明同时翻开两张纸牌.他们翻开的两张纸牌中只要出现笑脸就获奖.请问他们获奖的机会相等吗?判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.

(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥AC,AB=4,BC=![]() ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人去水果批发市场采购猕猴桃,他看中了A、B两家猕猴桃.这两家猕猴桃品质一样,零售价都为6元/千克,批发价各不相同,
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
数量范围 (千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发600千克猕猴桃,则他在A 、B两家批发分别需要多少元?
(2)如果他批发x千克猕猴桃(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发1800千克猕猴桃,你能帮助他选择在哪家批发更优惠吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱底面半径为![]() cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A. 12cm B. ![]() cm C. 15cm D.
cm C. 15cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,在平面直角坐标系中,点 A 为 x 轴负半轴上一点,点 B 为 x 轴正半轴上一点,C(0,﹣2),D(﹣3,﹣2).


(1)AB,CD 的位置关系为 ;△BCD 的面积为 ;S△ACD S△BCD(填两者之间的数量关系);
(2)如图 1,若∠1=100°,∠ACB=65°,求∠CAB 的度数;
(3)如图 2,若∠ADC=∠DAC,∠ACB 的平分线 CE 交 DA 的延长线于点 E,在 B 点的运动过程中![]() 的值是否变化?若不变,直接写出其值;若变化,请说明理由.(注:三角形内角和等于 180°)
的值是否变化?若不变,直接写出其值;若变化,请说明理由.(注:三角形内角和等于 180°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,妈妈下班后从公司开车回家,途中想起忘了带第二天早上开早会的一个文件夹,于是打电话让办公室王阿姨马上从公司送来,同时妈妈也往回开,遇到王阿姨后停下说了几句话,接着继续开车回家.设妈妈从公司出发后所用时间为t,妈妈与家的距离为s.下面能反映s与t的函数关系的大致图象是( )
A.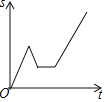 B.
B.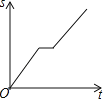
C. D.
D.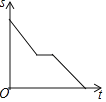
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com