
【题目】如图⊙O是△ABC的外接圆,圆心O在这个三角形的高AD上,AB=10,BC=12,求⊙O的半径.
【答案】解:如图,连接OB.
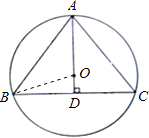
∵AD是△ABC的高.
∴BD= ![]() BC=6
BC=6
在Rt△ABD中,AD= ![]() =
= ![]() =8.
=8.
设圆的半径是R.
则OD=8﹣R.
在Rt△OBD中,根据勾股定理可以得到:R2=36+(8﹣R)2
解得:R= ![]() .
.
【解析】连接OB,根据垂经定理求出BD的长,在Rt△ABD中由勾股定理求得AD=8,设圆的半径是R,则OD=8-R,在Rt△OBD中由勾股定理可求得R的值.解答此题的关键是作出辅助线OB.注意:垂径定理和勾股定理常常在一起中应用.
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某机械厂甲、乙两个生产车间承担生产同一种零件的任务,甲、乙两车间共有![]() 人,甲车间平均每人每天生产零件
人,甲车间平均每人每天生产零件![]() 个.乙车间平均每人每天生产零件
个.乙车间平均每人每天生产零件![]() 个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为
个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为![]() 个.
个.
(1)求甲、乙两车间各有多少人?
(2)该机械厂改进了生产技术.在甲、乙两车间总人数不变的情况下,从甲车间调出一部分人到乙车间.调整后甲车间平均每人每天生产零件![]() 个,乙车间平均每人每天生产零件
个,乙车间平均每人每天生产零件![]() 个,若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于
个,若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于![]() 个,求从甲车间最多调出多少人到乙车间.
个,求从甲车间最多调出多少人到乙车间.
查看答案和解析>>
科目:初中数学 来源: 题型:
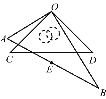
【题目】将一副三角板按如图所示的方式叠放在一起,两直角顶点重合于点O.
(1)求∠AOD+∠BOC的度数;
(2)当AB的中点E恰好落在CD的中垂线上时,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),抛物线y=x2﹣2x+k与x轴交于A,B两点,与y轴交于点C(0,﹣3).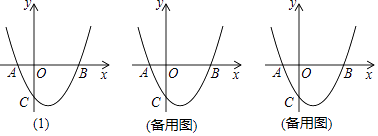
(1)k= , 点A的坐标为 , 点B的坐标为;
(2)设抛物线y=x2﹣2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)在抛物线y=x2﹣2x+k上求出点Q坐标,使△BCQ是以BC为直角边的直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人去水果批发市场采购猕猴桃,他看中了A、B两家猕猴桃.这两家猕猴桃品质一样,零售价都为6元/千克,批发价各不相同,
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
数量范围 (千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发600千克猕猴桃,则他在A 、B两家批发分别需要多少元?
(2)如果他批发x千克猕猴桃(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发1800千克猕猴桃,你能帮助他选择在哪家批发更优惠吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
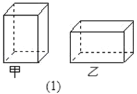
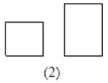
【题目】某纸品加工厂利用边角料裁出正方形和长方形两种硬纸片,长方形的宽与正方形的边长相等(如图2),再将它们制作成甲乙两种无盖的长方体小盒(如图1).现将300张长方形硬纸片和150张正方形硬纸片全部用于制作这两种小盒,可以做成甲乙两种小盒各多少个?(注:图1中向上的一面无盖)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com