
【题目】某机械厂甲、乙两个生产车间承担生产同一种零件的任务,甲、乙两车间共有![]() 人,甲车间平均每人每天生产零件
人,甲车间平均每人每天生产零件![]() 个.乙车间平均每人每天生产零件
个.乙车间平均每人每天生产零件![]() 个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为
个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为![]() 个.
个.
(1)求甲、乙两车间各有多少人?
(2)该机械厂改进了生产技术.在甲、乙两车间总人数不变的情况下,从甲车间调出一部分人到乙车间.调整后甲车间平均每人每天生产零件![]() 个,乙车间平均每人每天生产零件
个,乙车间平均每人每天生产零件![]() 个,若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于
个,若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于![]() 个,求从甲车间最多调出多少人到乙车间.
个,求从甲车间最多调出多少人到乙车间.
【答案】(1)甲车间有30人,乙车间有20人;(2)从甲车间最多调出7人到乙车间.
【解析】
(1)设甲、乙两车间各有x、y人,根据甲、乙两车间共有50人和甲车间每天生产零件总数与乙车间每天生产零件总数之和为1300个列方程组求出x、y的值即可得答案;
(2)设从甲车间调出a人到乙车间,表示出两个车间的人数,根据生产零件总数之和不少于1480个列出不等式,解不等式即可得答案.
(1)设甲车间有x人,乙车间有y人,
根据题意得:![]() ,
,
解得:![]() .
.
答:甲车间有30人,乙车间有20人.
(2)设从甲车间调出a人到乙车间,则甲车间有(30-a)人,乙车间有(20+a)人,
∵甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于![]() 个,
个,
∴35(30-a)+25(20+a)≥1480,
解得:a≤7.
答:从甲车间最多调出7人到乙车间.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,F是边AB,BC上一动点,DE⊥DF,且DE=DF,M为EF的中点.
(1)当点F在边AB上时(如图①).
①求证:点E在直线BC上;
②若BF=2,则MC的长为多少.
(2)当点F在BC上时(如图②),求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则点P到AB间的距离是 . 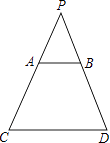
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O是坐标原点,点A在y轴的正半轴上,坐标为![]() ,点B在x轴的负半轴上,坐标为
,点B在x轴的负半轴上,坐标为![]() ,同时
,同时![]() 满足
满足![]() ,连接AB,且AB=10.点D是x轴正半轴上的一个动点,点E是线段AB上的一个动点,连接DE.
,连接AB,且AB=10.点D是x轴正半轴上的一个动点,点E是线段AB上的一个动点,连接DE.

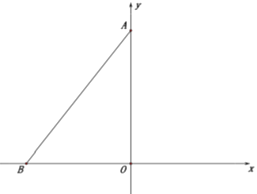
(1)求A、B两点坐标;
(2)若![]() ,点D的横坐标为x,线段
,点D的横坐标为x,线段![]() 的长为d,请用含x的式子表示d;
的长为d,请用含x的式子表示d;
(3)若![]() ,AF、DF分别平分∠BAO、∠BDE,相交于点F,求∠F的度数.
,AF、DF分别平分∠BAO、∠BDE,相交于点F,求∠F的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织七年级学生参加夏令营,已知:用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人,现有学生400人,计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)请你帮学校设计出所有的租车方案;
(3)若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的方案,并求出最省租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
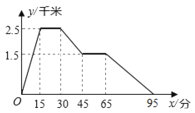
【题目】如图所示:图象中所反映的过程是:小冬从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x轴表示时间,y轴表示小冬离家的距离.根据图象提供的信息,下列说法正确的有________.
①.体育场离小冬家2.5千米 ②.小冬在体育场锻炼了15分钟
③.体育场离早餐店4千米 ④.小冬从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com