
【题目】已知四边形ABCD是正方形,F是边AB,BC上一动点,DE⊥DF,且DE=DF,M为EF的中点.
(1)当点F在边AB上时(如图①).
①求证:点E在直线BC上;
②若BF=2,则MC的长为多少.
(2)当点F在BC上时(如图②),求![]() 的值.
的值.

【答案】(1)①证明见解析;②![]() ;(2)
;(2) ![]() .
.
【解析】
(1)①连接CE,证明△ADF≌△CDE,得到∠DCE=∠DAF=90°即可;
②作FK∥MC,证明CM=![]() FK,求出FK=
FK,求出FK=![]() BF即可;
BF即可;
(2)过点E作CD的平行线分别交AD、BC的延长线于K、Q,EN∥MC,根据平行线等分线段定理即可解答.
(1)①证明:如图①,连接CE.
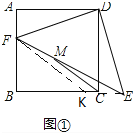
∵DE⊥DF,∴∠FDE=90°.
∵四边形ABCD是正方形,
∴∠ADC=∠DAF=∠DCB=90°,
DA=DC.
∴∠ADC-∠FDC=∠FDE-∠FDC,
即∠ADF=∠CDE.
又∵DF=DE,
∴△DAF≌△DCE(SAS).
∴∠DAF=∠DCE=90°,
∴∠DCE+∠DCB=180°.
∴点E在直线BC上.
②如图①,作FK∥MC,∵M为EF的中点,
∴CM=![]() FK,
FK,
∵∠DMB=∠DCB=90°,
∴D、M、C、B四点共圆,
∴∠MCD=∠MBD=45°,
∴∠BKF=45°,
∵BF=2,∴FK=2![]() ,
,
∴CM=![]() FK=
FK=![]() ;
;
(2) 过点E作CD的平行线分别交AD、BC的延长线于K、G,EN∥MC,
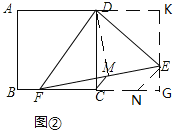
∵M为EF的中点,
∴CM=![]() NE,FC=CN,
NE,FC=CN,
∴NG=EG=BF,
![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
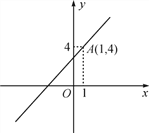
【题目】如图,已知,一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的解析式;
(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰Rt△ABC的直角边为1,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边.画第三个Rt△ADE,…,依此类推直到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为 . 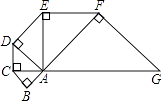
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校体育社团在校内开展“你最喜欢的体育项目是什么?![]() 四项选一项
四项选一项![]() ”调查,对九年级学生随机抽样,并将收集的数据绘制成如下两幅不完整的统计图.请结合统计图,解答下列问题:
”调查,对九年级学生随机抽样,并将收集的数据绘制成如下两幅不完整的统计图.请结合统计图,解答下列问题:

(1)本次抽样人数有________人;
(2)补全条形统计图和扇形统计图;
(3)该校九年级共有600名学生,估计九年级最喜欢跳绳项目的学生有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A,B两点,与反比例函数 ![]() 的图象交于C,D两点,DE⊥x轴于点E,已知C点的坐标是(6,﹣1),DE=3.
的图象交于C,D两点,DE⊥x轴于点E,已知C点的坐标是(6,﹣1),DE=3.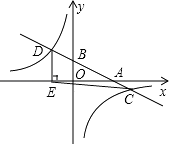
(1)求反比例函数与一次函数的解析式;
(2)求△CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动.同时动点Q从点C出发,沿线段CD向点D运动.点P,Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.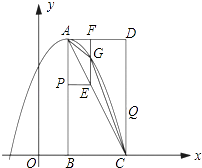
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少?
(3)在动点P,Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机械厂甲、乙两个生产车间承担生产同一种零件的任务,甲、乙两车间共有![]() 人,甲车间平均每人每天生产零件
人,甲车间平均每人每天生产零件![]() 个.乙车间平均每人每天生产零件
个.乙车间平均每人每天生产零件![]() 个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为
个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为![]() 个.
个.
(1)求甲、乙两车间各有多少人?
(2)该机械厂改进了生产技术.在甲、乙两车间总人数不变的情况下,从甲车间调出一部分人到乙车间.调整后甲车间平均每人每天生产零件![]() 个,乙车间平均每人每天生产零件
个,乙车间平均每人每天生产零件![]() 个,若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于
个,若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于![]() 个,求从甲车间最多调出多少人到乙车间.
个,求从甲车间最多调出多少人到乙车间.
查看答案和解析>>
科目:初中数学 来源: 题型:
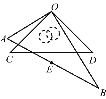
【题目】将一副三角板按如图所示的方式叠放在一起,两直角顶点重合于点O.
(1)求∠AOD+∠BOC的度数;
(2)当AB的中点E恰好落在CD的中垂线上时,求∠AOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com