
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动.同时动点Q从点C出发,沿线段CD向点D运动.点P,Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.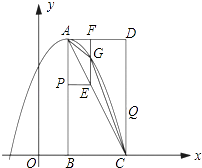
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少?
(3)在动点P,Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.
【答案】
(1)A(1,4).
由题意知,可设抛物线解析式为y=a(x﹣1)2+4
∵抛物线过点C(3,0),
∴0=a(3﹣1)2+4,
解得,a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3.
(2)解:∵A(1,4),C(3,0),
∴可求直线AC的解析式为y=﹣2x+6.
∵点P(1,4﹣t).
∴将y=4﹣t代入y=﹣2x+6中,解得点E的横坐标为x=1+ ![]() .
.
∴点G的横坐标为1+ ![]() ,代入抛物线的解析式中,可求点G的纵坐标为4﹣
,代入抛物线的解析式中,可求点G的纵坐标为4﹣ ![]() .
.
∴GE=(4﹣ ![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣ ![]() .
.
又∵点A到GE的距离为 ![]() ,C到GE的距离为2﹣
,C到GE的距离为2﹣ ![]() ,
,
即S△ACG=S△AEG+S△CEG= ![]() EG
EG ![]() +
+ ![]() EG(2﹣
EG(2﹣ ![]() )
)
= ![]() 2(t﹣
2(t﹣ ![]() )=﹣
)=﹣ ![]() (t﹣2)2+1.
(t﹣2)2+1.
当t=2时,S△ACG的最大值为1.
(3)解:第一种情况如图1所示,点H在AC的上方, 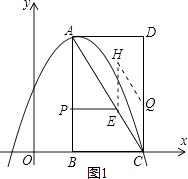
由四边形CQEH是菱形知CQ=CE=t,
根据△APE∽△ABC,知
![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得t=20﹣8
,解得t=20﹣8 ![]() ;
;
第二种情况如图2所示,点H在AC的下方, 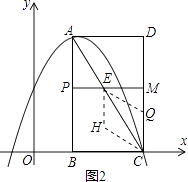
由四边形CQHE是菱形知CQ=QE=EH=HC=t,PE= ![]() t,EM=2﹣
t,EM=2﹣ ![]() t,MQ=4﹣2t.
t,MQ=4﹣2t.
则在直角三角形EMQ中,根据勾股定理知EM2+MQ2=EQ2,即(2﹣ /span>![]() t)2+(4﹣2t)2=t2,
t)2+(4﹣2t)2=t2,
解得,t1= ![]() ,t2=4(不合题意,舍去).
,t2=4(不合题意,舍去).
综上所述,t=20﹣8 ![]() 或t=
或t= ![]() .
.
【解析】(1)由抛物线过点C(3,0),求出抛物线的解析式为y=﹣x2+2x+3;(2)由A(1,4),C(3,0),可求出直线AC的解析式;又点P(1,4﹣t),解得点E的横坐标为x=1+ ![]() ,所以点G的横坐标为1+
,所以点G的横坐标为1+ ![]() ,代入抛物线的解析式中,可求点G的纵坐标为4﹣
,代入抛物线的解析式中,可求点G的纵坐标为4﹣ ![]() ,得到GE=(4﹣
,得到GE=(4﹣ ![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣ ![]() ,又点A到GE的距离为
,又点A到GE的距离为 ![]() ,C到GE的距离为2﹣
,C到GE的距离为2﹣ ![]() ,即S△ACG=S△AEG+S△CEG,求出S△ACG的最大值为;(3)第一种情况如图1所示,点H在AC的上方,由四边形CQEH是菱形知CQ=CE=t,根据△APE∽△ABC
,即S△ACG=S△AEG+S△CEG,求出S△ACG的最大值为;(3)第一种情况如图1所示,点H在AC的上方,由四边形CQEH是菱形知CQ=CE=t,根据△APE∽△ABC![]() ,得到比例,求出t的值;第二种情况如图2所示,点H在AC的下方,由四边形CQHE是菱形知CQ=QE=EH=HC=t,PE=
,得到比例,求出t的值;第二种情况如图2所示,点H在AC的下方,由四边形CQHE是菱形知CQ=QE=EH=HC=t,PE= ![]() t,EM=2﹣
t,EM=2﹣ ![]() t,MQ=4﹣2t.则在直角三角形EMQ中,根据勾股定理知EM2+MQ2=EQ2,求出t的值 ;此题是综合题,难度较大,计算和解方程时需认真仔细.
t,MQ=4﹣2t.则在直角三角形EMQ中,根据勾股定理知EM2+MQ2=EQ2,求出t的值 ;此题是综合题,难度较大,计算和解方程时需认真仔细.


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,﹣3),
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由;
(3)平行于x轴的一条直线交抛物线于M、N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,F是边AB,BC上一动点,DE⊥DF,且DE=DF,M为EF的中点.
(1)当点F在边AB上时(如图①).
①求证:点E在直线BC上;
②若BF=2,则MC的长为多少.
(2)当点F在BC上时(如图②),求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】D,E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB,AC的中点.O是△ABC所在平面上的动点,连接OB,OC,点G,F分别是OB,OC的中点,顺次连接点D,G,F,E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则点P到AB间的距离是 . 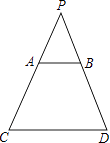
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织七年级学生参加夏令营,已知:用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人,现有学生400人,计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)请你帮学校设计出所有的租车方案;
(3)若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的方案,并求出最省租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2019次运动后,动点P的坐标是( )

A. (2018,0)B. (2018,2)C. (2019,2)D. (2019,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com