
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.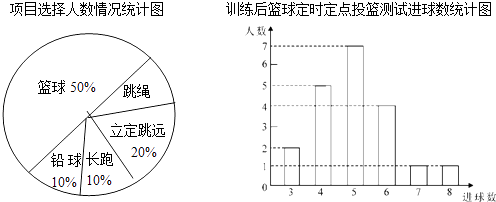
请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为度,该班共有学生人,训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
【答案】
(1)36,40,5
(2)解:三名男生分别用A1,A2,A3表示,一名女生用B表示.根据题意,可画树形图如下:
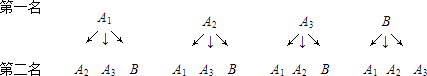
由上图可知,共有12种等可能的结果,选中两名学生恰好是两名男生(记为事件M)的结果有6种,
∴P(M)= ![]() =
= ![]() .
.
【解析】解:(1)扇形图中跳绳部分的扇形圆心角为360°×(1﹣50%﹣20%﹣10%﹣10%)=36度;
该班共有学生(2+5+7+4+1+1)÷50%=40人;
训练后篮球定时定点投篮平均每个人的进球数是 ![]() =5,
=5,
故答案为:36,40,5.
(1)圆心角=360°![]() 百分比;(2)事件分两个步骤,树状图分两层,关注的结果有6种,机会均等的结果有12种,二者相除即可.
百分比;(2)事件分两个步骤,树状图分两层,关注的结果有6种,机会均等的结果有12种,二者相除即可.


科目:初中数学 来源: 题型:
【题目】阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{﹣1,2,3}=![]() =
=![]() ;min{﹣1,2,3}=﹣1;min{﹣1,2,a}=
;min{﹣1,2,3}=﹣1;min{﹣1,2,a}=![]()
解决下列问题:
(1)若min{2,2x+2,4﹣2x}=2,则x的范围__________;
(2)①如果M{2,x+1,2x}=min{2,x+1,2x},求x;
②根据①,你发现了结论“如果M{a,b,c}=min{a,b,c},那么__________(填a,b,c的大小关系)”.
③运用②的结论,若M{2x+y+2,x+2y,2x﹣y}=min{2x+y+2,x+2y,2x﹣y},求x+y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
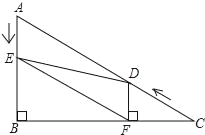
【题目】如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)DF= ;(用含t的代数式表示)
(2)求证:△AED≌△FDE;
(3)当t为何值时,△DEF是等边三角形?说明理由;
(4)当t为何值时,△DEF为直角三角形?(请直接写出t的值.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x+x﹣1的图象如图所示,下列对该函数性质的论断不可能正确的是( )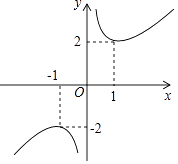
A.该函数的图象是中心对称图形
B.当x>0时,该函数在x=1时取得最小值2
C.在每个象限内,y的值随x值的增大而减小
D.y的值不可能为1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与点A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F、D.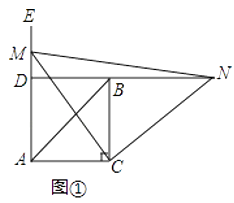
(1)问题发现:直接写出∠NDE=度;
(2)拓展探究:试判断,如图②当∠EAC为钝角时,其他条件不变,∠NDE的大小有无变化?请给出证明.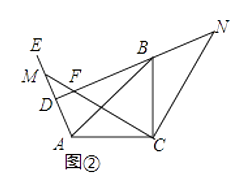
(3)如图③,若∠EAC=15°,BD= ![]() ,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.
,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.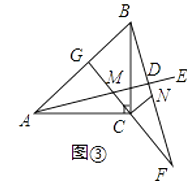
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() .小明将一个含
.小明将一个含![]() 的直角三角板
的直角三角板![]() 如图1所示放置,使顶点
如图1所示放置,使顶点![]() 落在直线
落在直线![]() 上,过点
上,过点![]() 作直线
作直线![]() 交直线
交直线![]() 于点
于点![]() (点
(点![]() 在
在![]() 左侧).
左侧).

(1)若![]() ,
,![]() ,则
,则![]() __________
__________![]() .
.
(2)若![]() 的角平分线交直线
的角平分线交直线![]() 于点
于点![]() ,如图2.
,如图2.
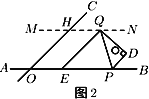

①当![]() ,
,![]() 时,求证:
时,求证:![]() .
.
②小明将三角板保持![]() 并向左平移,运动过程中,
并向左平移,运动过程中,![]() __________.(用
__________.(用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两市相距150千米,分别从A,B处测得国家级风景区中心C处的方向角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州市政府计划投资百亿元开发瓯江口新区,打造出一个“东方时尚岛、海上新温州”.为了解温州市民对瓯江口新区的关注情况,某学校数学兴趣小组随机采访部分温州市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | m | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | n |
D.不知道 | 50 | 0.25 |
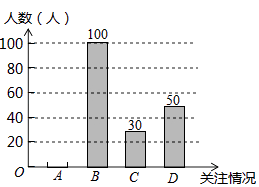
(1)根据上述统计表可得此次采访的人数为人;m= , n=;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,估计25000名温州市民中高度关注瓯江口新区的市民约人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com