
【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与点A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F、D.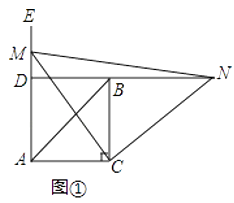
(1)问题发现:直接写出∠NDE=度;
(2)拓展探究:试判断,如图②当∠EAC为钝角时,其他条件不变,∠NDE的大小有无变化?请给出证明.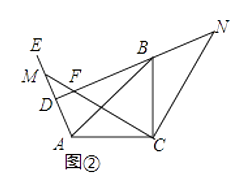
(3)如图③,若∠EAC=15°,BD= ![]() ,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.
,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.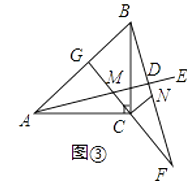
【答案】
(1)90
(2)解:∠NDE的大小不变,
在△MAC和△NBC中,
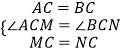 ,
,
∴△MAC≌△NBC,
∴∠N=∠AMC,
又∵∠MFD=∠NFC,
∴∠MDF=∠FCN=90°,
即∠NDE=90°
(3)解:AC=2,
在△MAC和△NBC中,
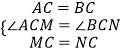 ,
,
∴△MAC≌△NBC,
∴∠NBC=∠MAC=15°,
如图③,设BC与AD交于点H,
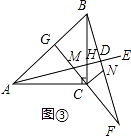
又∵∠AHC=∠BHD,
∴∠BDH=∠ACH=90°,
∴在Rt△ABD中,∠ABD=∠ABC+∠NBC=45°+15°=60°
∵BD= ![]() ,
,
∴AB=2 ![]() ,
,
∴AC=ABcos45°=2.
【解析】解:(1)∵∠ACB=90°,∠MCN=90°,
∴∠ACM=∠BCN,
在△MAC和△NBC中,
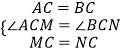 ,
,
∴△MAC≌△NBC,
∴∠NBC=∠MAC=90°,
又∵∠ACB=90°,∠EAC=90°,
∴∠NDE=90°.
所以答案是:90.
【考点精析】通过灵活运用旋转的性质,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.


科目:初中数学 来源: 题型:
【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A.平行四边形的对角线互相平分
B.有两对邻角互补的四边形为平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.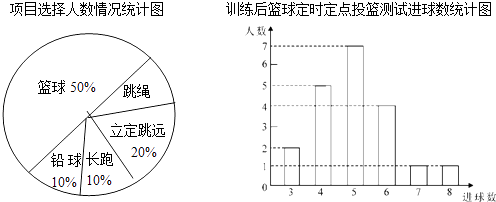
请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为度,该班共有学生人,训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某仓库有甲、乙、丙三辆运货车,每辆车只负责进货或出货,其中丙车每小时的运输量最多,乙车每小时的运输量最少,且乙车每小时的运输量为6吨.如图是从早晨上班开始库存量y(吨)与时间x(小时)的函数图像,OA段只有甲、丙车工作,AB段只有乙、丙车工作,BC段只有甲、乙车工作.
(1)你能确定甲、乙、丙三辆车哪辆是出货车吗?并说明理由.
(2)若甲、乙、丙三辆车一起工作,一天工作8小时,则仓库的库存量增加多少?
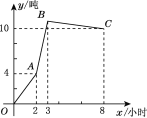
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程x2+mx+n=0有两个不相等实数根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com