
【题目】【发现证明】如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.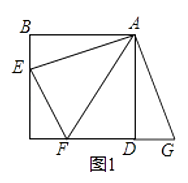
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
(1)【类比引申】如图2,点E,F分别在正方形ABCD的边CB,CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF,BE,DF之间的数量关系,并证明;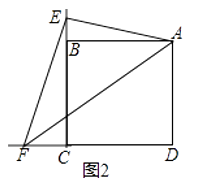
(2)【联想拓展】如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.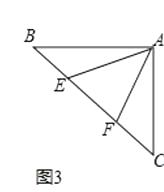
【答案】
(1)解:DF=EF+BE.
理由:如图1所示, 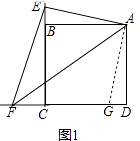 ∵AB=AD,
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∵∠ADC=∠ABE=90°,
∴点C、D、G在一条直线上,
∴EB=DG,AE=AG,∠EAB=∠GAD,
∵∠BAG+∠GAD=90°,
∴∠EAG=∠BAD=90°,
∵∠EAF=45°,
∴∠FAG=∠EAG﹣∠EAF=90°﹣45°=45°,
∴∠EAF=∠GAF,
在△EAF和△GAF中,
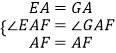 ,
,
∴△EAF≌△GAF,
∴EF=FG,
∵FD=FG+DG,
∴DF=EF+BE
(2)解:∵∠BAC=90°,AB=AC,
∴将△ABE绕点A顺时针旋转90°得△ACG,连接FG,如图2, 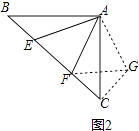
∴AG=AE,CG=BE,∠ACG=∠B,∠EAG=90°,
∴∠FCG=∠ACB+∠ACG=∠ACB+∠B=90°,
∴FG2=FC2+CG2=BE2+FC2;
又∵∠EAF=45°,
而∠EAG=90°,
∴∠GAF=90°﹣45°,
在△AGF与△AEF中,
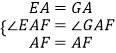 ,
,
∴△AEF≌△AGF,
∴EF=FG,
∴CF2=EF2﹣BE2=52﹣32=16,
∴CF=4.
【解析】(1)首先把△ABE绕点A逆时针旋转90°得到△ADG,然后再证明△AFE≌△AFG,依据全等三角形对应边相等可得到EF=FG,接下来,由FD=FG+DG可得到DF=EF+BE;
(2)首先将△ABE绕点A顺时针旋转90°得△ACG,连接FG,然后依据旋转的性质可得到AG=AE,CG=BE,∠ACG=∠B,∠EAG=90°,∠FCG=∠ACB+∠ACG=∠ACB+∠B=90°,接下来,再依据勾股定理可证明FG2=FC2+CG2=BE2+FC2,然后根据全等三角形的性质得到FG=EF,最后,再利用勾股定理可求得CF的长.
【考点精析】解答此题的关键在于理解图形的旋转的相关知识,掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素.


科目:初中数学 来源: 题型:
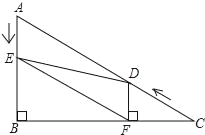
【题目】如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)DF= ;(用含t的代数式表示)
(2)求证:△AED≌△FDE;
(3)当t为何值时,△DEF是等边三角形?说明理由;
(4)当t为何值时,△DEF为直角三角形?(请直接写出t的值.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票.班长由王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动.你认为这个方法公平吗?请画树状图或列表,并说明理由.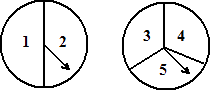
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x+x﹣1的图象如图所示,下列对该函数性质的论断不可能正确的是( )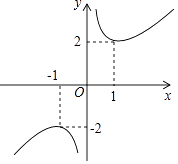
A.该函数的图象是中心对称图形
B.当x>0时,该函数在x=1时取得最小值2
C.在每个象限内,y的值随x值的增大而减小
D.y的值不可能为1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() .小明将一个含
.小明将一个含![]() 的直角三角板
的直角三角板![]() 如图1所示放置,使顶点
如图1所示放置,使顶点![]() 落在直线
落在直线![]() 上,过点
上,过点![]() 作直线
作直线![]() 交直线
交直线![]() 于点
于点![]() (点
(点![]() 在
在![]() 左侧).
左侧).

(1)若![]() ,
,![]() ,则
,则![]() __________
__________![]() .
.
(2)若![]() 的角平分线交直线
的角平分线交直线![]() 于点
于点![]() ,如图2.
,如图2.
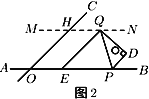

①当![]() ,
,![]() 时,求证:
时,求证:![]() .
.
②小明将三角板保持![]() 并向左平移,运动过程中,
并向左平移,运动过程中,![]() __________.(用
__________.(用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”
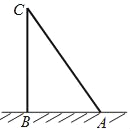
译文:“有一根竹子,原高二丈(1丈=10尺),现被风折断,竹梢触地面处与竹根的距离为6尺,问折断处离地面的高度为多少尺?”
如图,我们用点A,B,C分别表示竹梢,竹根和折断处,设折断处离地面的高度BC=x尺,则可列方程为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com