


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A.函数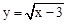 的自变量x的取值范围是x>3 的自变量x的取值范围是x>3 |
| B.菱形是中心对称图形,但不是轴对称图形 |
| C.一组对边平行,另一组对边相等四边形是平行四边形 |
| D.三角形的外心到三角形的三个顶点的距离相等 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
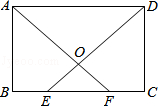
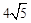 ,BC=4,向矩形ABCD外作△CDE,使△CDE为等腰三角形,且点E在边BC所在的直线上,请你画出图形,直接写出OE的长,并画出体现解法的辅助线.
,BC=4,向矩形ABCD外作△CDE,使△CDE为等腰三角形,且点E在边BC所在的直线上,请你画出图形,直接写出OE的长,并画出体现解法的辅助线.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com