练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

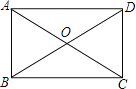
    【题目】如图，在矩形ABCD中，对角线AC与BD相交于O点，且AB=OA=2cm，则BD的长为 cm，BC的长为 cm．

    【答案】4，2．

    【解析】

    试题分析：根据矩形的性质得到OA=OC，OB=OD，AC=BD，∠ABC=90°，推出BD=AC=2OA=4，OA=OB=AB=2，得出等边△OAB，求出∠ACB=30°，根据勾股定理即可求出BC．

    解：∵矩形ABCD，

    ∴OA=OC，OB=OD，AC=BD，∠ABC=90°，

    ∴OA=OB，

    ∵AB=OA=2，

    ∴BD=AC=2OA=4，OA=OB=AB=2，

    ∴△OAB是等边三角形，

    ∴∠BAC=60°，

    ∴∠ACB=90°﹣60°=30°，

    由勾股定理得：BC===2．

    故答案为：4，2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠ACD=120°．

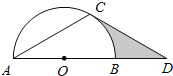
    （1）求证：CD是⊙O的切线；

    （2）若⊙O的半径为2，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

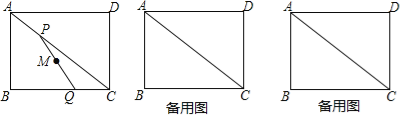
    【题目】如图，在矩形ABCD中，AB=3，BC=4，动点P以每秒一个单位的速度从点A出发，沿对角线AC向点C移动，同时动点Q以相同的速度从点C出发，沿边CB向点B移动．设P，Q两点移动时间为t秒（0≤t≤4）．

    （1）用含t的代数式表示线段PC的长是 ；

    （2）当△PCQ为等腰三角形时，求t的值；

    （3）以BQ为直径的圆交PQ于点M，当M为PQ的中点时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=3，BC=4，动点P以每秒一个单位的速度从点A出发，沿对角线AC向点C移动，同时动点Q以相同的速度从点C出发，沿边CB向点B移动．设P，Q两点移动时间为t秒（0≤t≤4）．

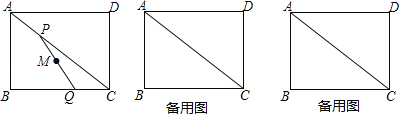
    （1）用含t的代数式表示线段PC的长是 ；

    （2）当△PCQ为等腰三角形时，求t的值；

    （3）以BQ为直径的圆交PQ于点M，当M为PQ的中点时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

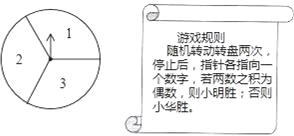
    【题目】如图所示，可以自由转动的转盘被3等分，指针落在每个扇形内的机会均等．

    （1）现随机转动转盘一次，停止后，指针指向1的概率为 ；

    （2）小明和小华利用这个转盘做游戏，若采用下列游戏规则，你认为对双方公平吗？请用列表或画树状图的方法说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

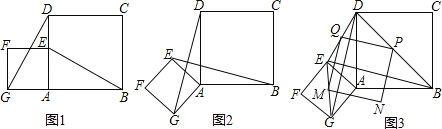
    【题目】如图1所示，四边形AEFG与四边形ABCD是正方形，其中G、A、B三点在同一直线上．连接DG、BE．完成下面问题：

    （1）求证：BE=DG；

    （2）如图2，将正方形AEFG绕点A逆时针转过一定角度时，小明发现：BE=DG且BE⊥DG，请你帮助小明证明这两个结论；

    （3）如图3，小明还发现：在旋转过程中，分别连接EG、GB、BD、DE的中点，得到的四边形MNPQ是正方形．若AB=a，AE=b其中a＞b，你能帮小明求出正方形MNPQ的面积的范围吗？写出过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知三角形两边的长分别是4和10，则此三角形第三边的长可能是(　　)

    A．5 B． 6 C．11 D．16

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】命题“全等三角形的面积相等”的条件是____________________，结论是______________________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：

    （1）请估计：当n很大时，摸到白球的频率将会接近 ；（精确到0.1）

    （2）假如你摸一次，你摸到白球的概率P（白球）= ；

    （3）试估算盒子里黑、白两种颜色的球各有多少只？

    查看答案和解析>>

    同步练习册答案