
【题目】已知:A是以BC为直径的圆上的一点,BE是⊙O的切线,CA的延长线与BE交于E点,F是BE的中点,延长AF,CB交于点P. 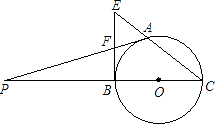
(1)求证:PA是⊙O的切线;
(2)若AF=3,BC=8,求AE的长.
【答案】
(1)证明:连接AB,OA,OF;
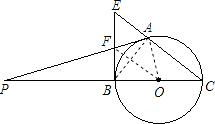
∵F是BE的中点,
∴FE=BF.
∵OB=OC,
∴OF∥EC.
∴∠C=∠POF.
∴∠AOF=∠CAO.
∵∠C=∠CAO,
∴∠POF=∠AOF.
∵BO=AO,OF=OF,
∴∠OAP=∠EBC=90°.
∴PA是⊙O的切线
(2)解:∵BE是⊙O的切线,PA是⊙O的切线,
∴BF=AF=3,
∴BE=6.
∵BC=8,∠CBE=90°,
∴CE=10.
∵BE是⊙O的切线,
∴EB2=AEEC.
∴AE=3.6.
【解析】(1)要想证PA是⊙O的切线,只要连接OA,求证∠OAP=90°即可;(2)先由切线长定理可知BF=AF,再在RT△BCE中根据勾股定理求出CE,最后由切割线定理求出AE的长.
【考点精析】本题主要考查了切线的判定定理的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角顶点的坐标为 ( )
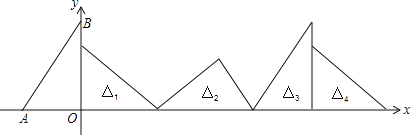
A. 8065 B. 8064 C. 8063 D. 8062
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=![]() ,求CG的长度;
,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚与小亮一起玩一种转盘游戏,图是两个完全相同的转盘,每个转盘分成面积相等的三个区域,分别用“1”,“2”,“3”表示.固定指针,同时转动两个转盘,任其自由停止. 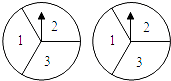
(1)用树状图或者列表法表示所有可能的结果;
(2)求两指针指的数字之和等于4的概率;
(3)若两指针指的数字都是奇数,则小刚获胜;否则,小亮获胜.游戏公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
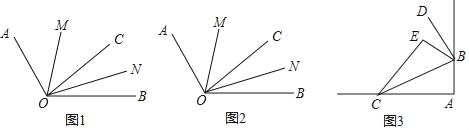
如图1,在∠AOB的内部有一条射线OC把∠AOB分成两个角,射线OM、ON分别平分∠AOC、∠BOC,试探究∠MON与∠AOB之间的数量关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论:
①请你在下表中填上当∠AOB为60°、90°、120°时∠MON的大小:
∠AOB的度数 | 60° | 90° | 120° |
∠MON的度数 |
|
|
|
②探索发现:无论∠AOB的度数是多少,∠MON与∠AOB的数量关系是不变的,请你直接写出结论:
∠MON ∠AOB.
(2)特例启发,解答题目:
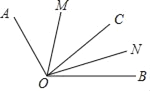
如图2,如果∠AOB=α,请你求∠MON的大小(用α表示).
(3)拓展结论,设计新题:
如图3,把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,求∠CBD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53). 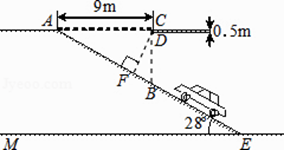
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】往一个长25m,宽11m的长方体游泳池注水,水位每小时上升0.32m,
(1)写出游泳池水深d(m)与注水时间x(h)的函数表达式;
(2)如果x(h)共注水y(m3),求y与x的函数表达式;
(3)如果水深1.6m时即可开放使用,那么需往游泳池注水几小时?注水多少(单位:m3)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com