
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53). 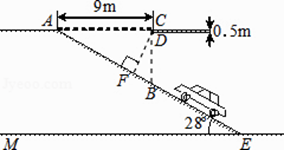
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A是以BC为直径的圆上的一点,BE是⊙O的切线,CA的延长线与BE交于E点,F是BE的中点,延长AF,CB交于点P. 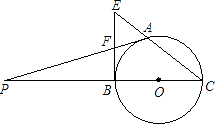
(1)求证:PA是⊙O的切线;
(2)若AF=3,BC=8,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38 ①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39 ②,
②一①得:3S―S=39-1,即2S=39-1,
∴S=![]() .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
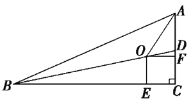
【题目】如图,在![]() ABC中,∠C=90,BD平分∠ABC,交AC于D,点O、E、F分别在BD、BC、
ABC中,∠C=90,BD平分∠ABC,交AC于D,点O、E、F分别在BD、BC、
AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
(1)如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D______(A,B)的好点,但点D______(B,A)的好点.(请在横线上填是或不是)知识运用:
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为-2.数______所表示的点是(M,N)的好点;
(3)如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过______秒时,P、A和B中恰有一个点为其余两点的好点?
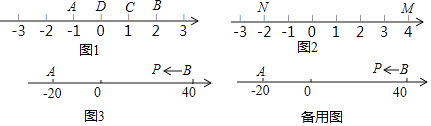
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
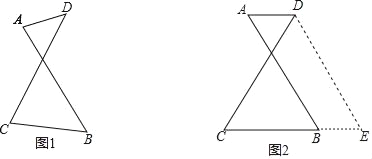
【题目】如图1有两条长度相等的相交线段AB、CD,它们相交的锐角中有一个角为60°,为了探究AD、CB与CD(或AB)之间的关系,小亮进行了如下尝试:
(1)在其他条件不变的情况下使得AD∥BC,如图2,将线段AB沿AD方向平移AD的长度,得到线段DE,然后联结BE,进而利用所学知识得到AD、CB与CD(或AB)之间的关系: ;(直接写出结果)
(2)根据小亮的经验,请对图1的情况(AD与CB不平行)进行尝试,写出AD、CB与CD(或AB)之间的关系,并进行证明;
(3)综合(1)、(2)的证明结果,请写出完整的结论: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD 中,点P在对角线AC上,过P作EF∥AB,HG∥AD,记四边形BFPH的面积为S1,四边形DEPG的面积为S2,则S1与S2的大小关系是( )
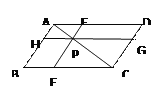
A. S1>S2 B. S1=S2 C. S1<S2 D. 无法判断
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com