
【题目】如图,直角△ABC中,∠A=90°,∠B=30°,AC=4,以A为圆心,AC长为半径画四分之一圆,则图中阴影部分的面积是(结果保留π). 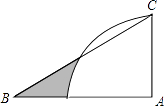
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,一条街道旁有A,B,C,D,E五幢居民楼,某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:
楼号 | A | B | C | D | E |
大桶水/桶 | 38 | 55 | 50 | 72 | 85 |
他计划在这五幢楼中租赁一间门市房,设立大桶水供应点,若仅考虑这五幢楼内的居民取水所走路程之和最小,则可以选择的地点应在( ).
![]()
A. B楼 B. C楼 C. D楼 D. E楼
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,O,B依次在直线MN上,如图1,现将射线OA绕点O顺时针方向以每秒10°的速度旋转,同时射线OB绕着点O按逆时针方向以每秒15°的速度旋转,直线MN保持不动,如图2,设旋转时间为t秒(t≤12).
(1)在旋转过程中,当t=2时,求∠AOB的度数.
(2)在旋转过程中,当∠AOB=105°时,求t的值.
(3)在旋转过程中,当OA或OB是某一个角(小于180°)的角平分线时,求t的值.
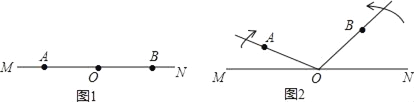
查看答案和解析>>
科目:初中数学 来源: 题型:
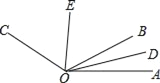
【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A是以BC为直径的圆上的一点,BE是⊙O的切线,CA的延长线与BE交于E点,F是BE的中点,延长AF,CB交于点P. 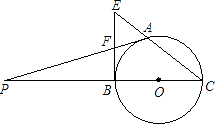
(1)求证:PA是⊙O的切线;
(2)若AF=3,BC=8,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.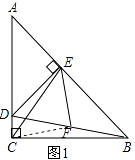
(1)若AD=3 ![]() ,BE=4,求EF的长;
,BE=4,求EF的长;
(2)求证:CE= ![]() EF;
EF;
(3)将图1中的△AED绕点A顺时针旋转,使AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
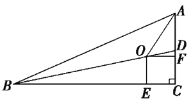
【题目】如图,在![]() ABC中,∠C=90,BD平分∠ABC,交AC于D,点O、E、F分别在BD、BC、
ABC中,∠C=90,BD平分∠ABC,交AC于D,点O、E、F分别在BD、BC、
AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
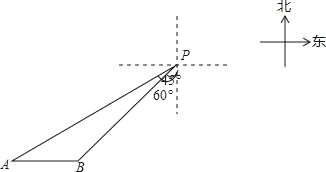
【题目】一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com