
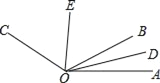
【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
【答案】(1) 65°’;(2) 150°;(3) ∠DOE=![]() ∠AOC,理由见解析
∠AOC,理由见解析
【解析】
(1)利用角平分线的定义得出∠AOD=∠BOD,∠BOE=∠COE,进而求出∠DOE的度数;
(2)根据角平分线的定义求出∠DOB和∠EOB的度数,代入∠DOE=∠DOB+∠EOB求出即可;
(3)根据角的和差关系求出∠AOC度数,再根据角平分线的定义求出∠DOB和∠EOB,代入∠DOE=![]() ∠BOC+∠AOB得出关系即可.
∠BOC+∠AOB得出关系即可.
(1)∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=![]() ∠BOC,∠BOE=∠COE=
∠BOC,∠BOE=∠COE=![]() ∠BOA,
∠BOA,
∵∠BOC=50°,∠BOA=80°,
∴∠BOD=25°,∠BOE=40°,
∴∠DOE=25°+40°=65°;
(2)∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=![]() ∠BOC,∠BOE=∠COE=
∠BOC,∠BOE=∠COE=![]() ∠BOA,
∠BOA,
∵∠AOC=150°,
∴∠DOE=∠DOB+∠EOB=![]() (∠BOC+∠BOA)=
(∠BOC+∠BOA)=![]() ∠AOC=75°;
∠AOC=75°;
(3)∠DOE=![]() ∠AOC;
∠AOC;
理由是:∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠AOD=∠BOD=![]() ∠BOC,∠BOE=∠COE=
∠BOC,∠BOE=∠COE=![]() ∠BOA,
∠BOA,
∴∠DOE=∠DOB+∠EOB=![]() (∠BOC+∠BOA)=
(∠BOC+∠BOA)=![]() ∠AOC.
∠AOC.


科目:初中数学 来源: 题型:
【题目】观察下列计算过程,发现规律,利用规律猜想并计算:
1+2=![]() =3;1+2+3=
=3;1+2+3=![]() =6,1+2+3+4=
=6,1+2+3+4=![]() =10;1+2+3+4+5=
=10;1+2+3+4+5=![]() =15;…
=15;…
(1)猜想:1+2+3+4+…+n= .
(2)利用上述规律计算:1+2+3+4+…+200;
(3)尝试计算:3+6+9+12+…3n的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC的中垂线DM交∠BAC的平分线AD于D, DE⊥AB于点E,DF⊥AC于F.连接DB、DC
(1)求证:△DBE≌△DFC.
(2)求证:AB+AC=2AE
(3)如图2,若△ABC的边BC的中垂线DM交∠BAC的外角平分线AD于D, DE⊥AB于点E,且AB>AC,写出AE、BE、AC之间的等量关系。(不需证明,只需在图2中作出辅助线、说明证哪两个三角形全等即可)。
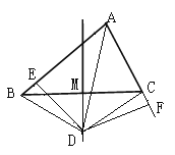
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k是不等于0的常数,反比例函数与二次函数在同一坐标系的大致图象如图,则它们的解析式可能分别是( ) 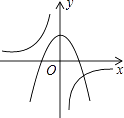
A.y=﹣ ![]() ,y=﹣kx2+k
,y=﹣kx2+k
B.y= ![]() ,y=﹣kx2+k
,y=﹣kx2+k
C.y= ![]() ,y=kx2+k
,y=kx2+k
D.y=﹣ ![]() ,y=﹣kx2﹣k
,y=﹣kx2﹣k
查看答案和解析>>
科目:初中数学 来源: 题型:
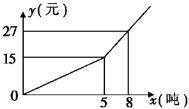
【题目】某市自来水公司为了鼓励市民节约用水,采取分段收费标准. 若某户居民每月应缴水费y(元)与用水量x(吨)的函数图象如图所示,
(1)分别写出x≤5和x>5的函数解析式;
(2)观察函数图象,利用函数解析式,回答自来水公司采取的收费标准;
(3)若某户居民六月交水费31元,则用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式,你发现了什么规律?
12=![]() ;12+22=
;12+22=![]() ;12+22+32=
;12+22+32=![]() ;12+22+32+42=
;12+22+32+42=![]() ;…
;…
①根据你发现的规律,计算下面算式的值;12+22+32+42+52=____________;
②请用一个含n的算式表示这个规律:12+22+32…+n2=___________;
③根据你发现的规律,计算下面算式的值:512+522+…+992+1002=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图1,点![]() ,
,![]() 在直线
在直线![]() 的同侧,在直线
的同侧,在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 的值最小.小明的思路是:如图2,作点
的值最小.小明的思路是:如图2,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,则
,则![]() 与直线
与直线![]() 的交点
的交点![]() 即为所求.
即为所求.
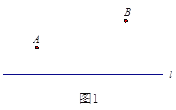
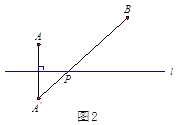
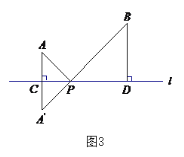
请你参考小明同学的思路,探究并解决下列问题:
(1)如图3,在图2的基础上,设![]() 与直线
与直线![]() 的交点为
的交点为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() . 若
. 若![]() ,
,![]() ,
,![]() ,写出
,写出![]() 的值为____________;
的值为____________;
(2)将(1)中的条件“![]() ”去掉,换成“
”去掉,换成“![]() ”,其它条件不变,写出此时
”,其它条件不变,写出此时![]() 的值 ___________;
的值 ___________;
(3)求![]() +
+![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com