
【题目】观察下列算式,你发现了什么规律?
12=![]() ;12+22=
;12+22=![]() ;12+22+32=
;12+22+32=![]() ;12+22+32+42=
;12+22+32+42=![]() ;…
;…
①根据你发现的规律,计算下面算式的值;12+22+32+42+52=____________;
②请用一个含n的算式表示这个规律:12+22+32…+n2=___________;
③根据你发现的规律,计算下面算式的值:512+522+…+992+1002=____________.
【答案】![]()
![]() 295425
295425
【解析】
(1) 根据所给的4个算式的规律, 12+22+32+42+52等于分母是6, 分子是5![]() 6
6![]() 11的分数的大小.
11的分数的大小.
(2) 根据所给的4个算式的规律, 12+22+32…+n2等于分母是6, 分子是n (n+1) (2n+1) 的分数的大小.
(3)用12+22+..+992+1002的值减去12+22+..+492+502的值, 求出算式512+522+..+992+1002的值是多少即可.
解:(1)12+22+32+42+52![]() ,
,
(2)12+22+32…+n2=![]() ,
,
(3) 512+522+..+992+1002=12+22+..+992+1002-(12+22+..+492+502)
=![]() =338350-42925=295425,
=338350-42925=295425,
故答案:295425.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)结合图象写出,0<x<4时,直接写出y的取值范围;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,求出矩形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
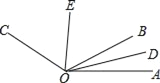
【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.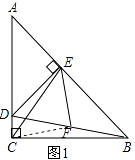
(1)若AD=3 ![]() ,BE=4,求EF的长;
,BE=4,求EF的长;
(2)求证:CE= ![]() EF;
EF;
(3)将图1中的△AED绕点A顺时针旋转,使AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个袋子中装有3个红球和2个黄球,这些球的形状、大小.质地完全相同,在看不到球的条件下,随机从袋子里同时摸出2个球,其中2个球的颜色相同的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
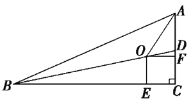
【题目】如图,在![]() ABC中,∠C=90,BD平分∠ABC,交AC于D,点O、E、F分别在BD、BC、
ABC中,∠C=90,BD平分∠ABC,交AC于D,点O、E、F分别在BD、BC、
AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的AD边上一个动点,矩形的两条边AB、BC长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )
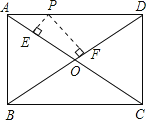
A. 4.8 B. 5 C. 6 D. 7.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗? 若能,求出两段铁丝的长度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
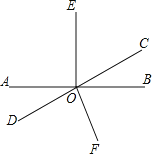
【题目】如图,已知直线AB与直线CD相交于点O,∠BOE=90°,FO平分∠BOD,∠BOC:∠AOC=1:3.
(1)求∠DOE、∠COF的度数.
(2)若射线OF、OE同时绕O点分别以2°/s、4°/s的速度,顺时针匀速旋转,当射线OE、OF的夹角为90°时,两射线同时停止旋转.设旋转时间为t,试求t值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com