
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)结合图象写出,0<x<4时,直接写出y的取值范围;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,求出矩形ABCD的周长.
【答案】
(1)
解:∵y=x2+(2m﹣1)x+m2﹣1经过坐标原点,
∴0=0+0+m2﹣1,即m2﹣1=0
解得m=±1.
又∵当x<0时,y随x的增大而减小,
∴m=﹣1,
∴二次函数解析式为y=x2﹣3x
(2)﹣ ![]() ≤y<4
≤y<4
(3)
解:如图2中,
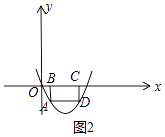
∵BC=1,B、C关于对称轴对称,
∴B(,1,0),C((2,0),
∵AB⊥x轴,DC⊥x轴,
∴A(1,﹣2),D(2,﹣2),
∴AB=DC=2,BC=AD=1,
∴四边形ABCD的周长为6,
当BC=1时,矩形的周长为6
【解析】解:(2)如图1中,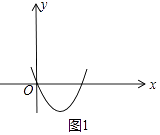
x=0时,y=0,
∵y=(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴x= ![]() 时,y最小值为﹣
时,y最小值为﹣ ![]() ,
,
x=4时,y=4,
∴0<x<4时,﹣ ![]() ≤y<4.
≤y<4.
所以答案是﹣ ![]() ≤y<4.
≤y<4.
【考点精析】通过灵活运用二次函数的图象,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知y-2与x+1成正比例函数关系,且x=-2时,y=6.
(1)写出y与x之间的函数解析式;
(2)求当x=-3时,y的值;
(3)求当y=4时,x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列计算过程,发现规律,利用规律猜想并计算:
1+2=![]() =3;1+2+3=
=3;1+2+3=![]() =6,1+2+3+4=
=6,1+2+3+4=![]() =10;1+2+3+4+5=
=10;1+2+3+4+5=![]() =15;…
=15;…
(1)猜想:1+2+3+4+…+n= .
(2)利用上述规律计算:1+2+3+4+…+200;
(3)尝试计算:3+6+9+12+…3n的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是2015年12月月历.
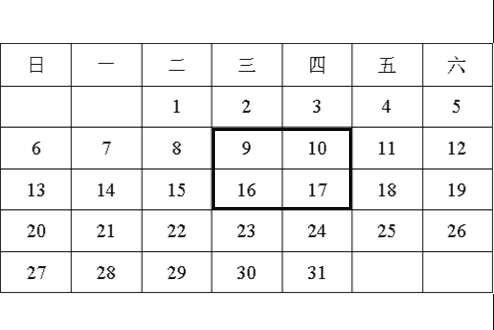
(1)如图,用一正方形框在表中任意框往4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是 , , .
(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2= .
(3)当(1)中被框住的4个数之和等于76时,x的值为多少?
(4)在(1)中能否框住这样的4个数,它们的和等于92?若能,则求出x的值;若不能,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①) 
阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求间径就是要求⊙O的直径.
(1)再次阅读后,发现AB=寸,CD=寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件.
(2)帮助小智求出⊙O的直径 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣ ![]() +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣
+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣ ![]() +bx+c的图象分别交于B,C两点,点B在第一象限.
+bx+c的图象分别交于B,C两点,点B在第一象限.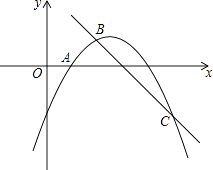
(1)求二次函数y=﹣ ![]() +bx+c的表达式;
+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC的中垂线DM交∠BAC的平分线AD于D, DE⊥AB于点E,DF⊥AC于F.连接DB、DC
(1)求证:△DBE≌△DFC.
(2)求证:AB+AC=2AE
(3)如图2,若△ABC的边BC的中垂线DM交∠BAC的外角平分线AD于D, DE⊥AB于点E,且AB>AC,写出AE、BE、AC之间的等量关系。(不需证明,只需在图2中作出辅助线、说明证哪两个三角形全等即可)。
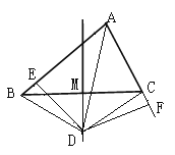
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式,你发现了什么规律?
12=![]() ;12+22=
;12+22=![]() ;12+22+32=
;12+22+32=![]() ;12+22+32+42=
;12+22+32+42=![]() ;…
;…
①根据你发现的规律,计算下面算式的值;12+22+32+42+52=____________;
②请用一个含n的算式表示这个规律:12+22+32…+n2=___________;
③根据你发现的规律,计算下面算式的值:512+522+…+992+1002=____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com