
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У����κ���y=�� ![]() +bx+c��ͼ����A��1��0�����ҵ�x=0��x=5ʱ����Ӧ�ĺ���ֵ��ȣ�һ�κ���y=��x+3����κ���y=��
+bx+c��ͼ����A��1��0�����ҵ�x=0��x=5ʱ����Ӧ�ĺ���ֵ��ȣ�һ�κ���y=��x+3����κ���y=�� ![]() +bx+c��ͼ��ֱ���B��C���㣬��B�ڵ�һ���ޣ�
+bx+c��ͼ��ֱ���B��C���㣬��B�ڵ�һ���ޣ�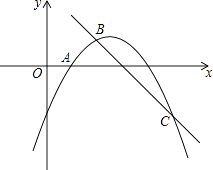
��1������κ���y=�� ![]() +bx+c�ı���ʽ��
+bx+c�ı���ʽ��
��2������AB����AB�ij���
��3������AC��M���߶�AC���е㣬����B�Ƶ�M��ת180��õ���N������AN��CN���ж��ı���ABCN����״����֤����Ľ��ۣ�
���𰸡�
��1��
�⣺��x=0ʱ��y=c������0��c����
�ɵ�x=0��x=5ʱ����Ӧ�ĺ���ֵ��ȣ��ã�5��c����
����5��c����1��0�����뺯������ʽ����
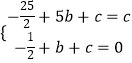 ��
��
��� 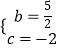 ��
��
�������ߵĽ���ʽΪy=�� ![]() x2+
x2+ ![]() x��2
x��2
��2��
�⣺������������ֱ�ߣ���
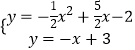 ��
��
��� ![]() ��
�� ![]() ��
��
��B��2��1����C��5����2����
�ɹ��ɶ�������
AB= ![]() =
= ![]()
��3��
�⣺��ͼ��
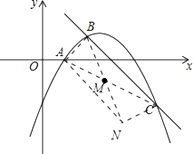 ��
��
�ı���ABCN��ƽ���ı��Σ�
֤������M��AC���е㣬
��AM=CM��
�ߵ�B�Ƶ�M��ת180��õ���N��
��BM=MN��
���ı���ABCN��ƽ���ı���
����������1�����ݵ�x=0��x=5ʱ����Ӧ�ĺ���ֵ��ȣ��ɵã�5��c�������ݴ���ϵ�������ɵú�������ʽ����2��������������ֱ�ߣ��ɵ÷����飬���ݽⷽ���飬�ɵ�B��C�����꣬���ݹ��ɶ������ɵ�AB�ij�����3�������߶��е�����ʣ��ɵ�M������꣬������ת�����ʣ��ɵ�MN��BM�Ĺ�ϵ������ƽ���ı��ε��ж����ɵô𰸣�
�����㾫����ͨ��������ö��κ�����ͼ��Ͷ��κ��������ʣ����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С�����Խ����⣮


 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���ֵ�����A��B��C��D��E�崱����¥��ij��Ͱˮ������ͳ�Ƹ�¥����ÿ�������Ͱˮ���������±�:
¥�� | A | B | C | D | E |
��Ͱˮ/Ͱ | 38 | 55 | 50 | 72 | 85 |
���ƻ������崱¥������һ�����з���������Ͱˮ��Ӧ���������������崱¥�ڵľ���ȡˮ����·��֮����С�������ѡ��ĵص�Ӧ��(����).
![]()
A. B¥ B. C¥ C. D¥ D. E¥
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������y=x2+��2m��1��x+m2��1��������ԭ�㣬�ҵ�x��0ʱ��y��x���������С��
��1���������ߵĽ���ʽ��
��2�����ͼ��д����0��x��4ʱ��ֱ��д��y��ȡֵ��Χ��
��3�����A�Ǹ���������λ��x���·���һ�����㣬����A��x���ƽ���߽�����������һ��D������AB��x���ڵ�B��DC��x���ڵ�C����BC=1ʱ���������ABCD���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����б����У�
���ɷ���![]() =2ȥ��ĸ����x��12=10��
=2ȥ��ĸ����x��12=10��
���ɷ���![]() x=
x=![]() ����ͬ����
����ͬ����![]() ����x=1��
����x=1��
���ɷ���6x��4=x+4�����7x=0��
���ɷ���2��![]() ����ͬ����6����12��x��5=3��x+3����
����ͬ����6����12��x��5=3��x+3����
������εĸ����ǣ�����������
A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�ACΪ�Խ��ߣ�EΪAB��һ�㣬����E��EF��AD����AC,DC�ֱ��ڵ�G��F��HΪCG���е㣬����DE��EH��DH��FH�����н����н�����ȷ���У� ��
��EG=DF��
�ڡ�AEH+��ADH=180�㣻
�ۡ�EHF�ա�DHC��
����![]() ����S��EDH=13S��CFH .
����S��EDH=13S��CFH .

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��O��B������ֱ��MN�ϣ���ͼ1���ֽ�����OA�Ƶ�O˳ʱ�뷽����ÿ��10�����ٶ���ת��ͬʱ����OB���ŵ�O����ʱ�뷽����ÿ��15�����ٶ���ת��ֱ��MN���ֲ�������ͼ2������תʱ��Ϊt�루t��12����
��1������ת�����У���t=2ʱ�����AOB�Ķ�����
��2������ת�����У�����AOB=105��ʱ����t��ֵ��
��3������ת�����У���OA��OB��ijһ���ǣ�С��180�����Ľ�ƽ����ʱ����t��ֵ��
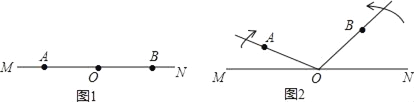
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
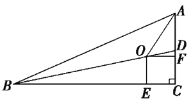
����Ŀ����ͼ����![]() ABC�У���C��90��BDƽ�֡�ABC����AC��D����O��E��F�ֱ���BD��BC��
ABC�У���C��90��BDƽ�֡�ABC����AC��D����O��E��F�ֱ���BD��BC��
AC�ϣ����ı���OECF��������.
��1����֤����O�ڡ�BAC��ƽ�����ϣ�
��2����AC��5��BC��12����OE�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com