
【题目】如图1,△ABC的边BC的中垂线DM交∠BAC的平分线AD于D, DE⊥AB于点E,DF⊥AC于F.连接DB、DC
(1)求证:△DBE≌△DFC.
(2)求证:AB+AC=2AE
(3)如图2,若△ABC的边BC的中垂线DM交∠BAC的外角平分线AD于D, DE⊥AB于点E,且AB>AC,写出AE、BE、AC之间的等量关系。(不需证明,只需在图2中作出辅助线、说明证哪两个三角形全等即可)。
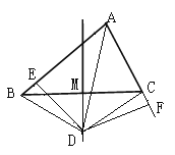
图1 图2
【答案】(1)见解析(2)见解析(3)BE=AE+AC
【解析】试题分析:(1)根据线段垂直平分线的性质得到DB=DC,根据角平分线的性质得到DE=DF,由全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到AE=AF,BE=CF,等量代换即可得到结论;
(3)如图2,过D作DN⊥AC,垂足为N,连接DB、DC,根据线段垂直平分线的性质和角平分线的性质得到DN=DE,DB=DC,推出Rt△DBE≌Rt△DCN(HL),根据全等三角形的性质得到BE=CN,由于Rt△DEA≌Rt△DNA(HL),根据全等三角形的性质得到AN=AE,等量代换即可得到结论.
(1)证明:∵DM垂直平分BC,
∴DB=DC,
∵∠1=∠2,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△DEB与Rt△DFC中,
![]() ,
,
∴Rt△DEB≌Rt△DFC;
(2)∵∠AED=∠AFD=90°,
在Rt△ADE≌Rt△ADF中,
![]() ,
,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
又∵Rt△DEB≌Rt△DFC,
∴BE=CF,
∴AB+AC=AE+BE+AF﹣CF=2AE;
(3)BE=AE+AC.
证明:如图2,过D作DN⊥AC,垂足为N,连接DB、DC,
则DN=DE,DB=DC,
又∵DE⊥AB,DN⊥AC,
∴∠DEB=∠DNC=90°,
在Rt△DBE和Rt△DCN中,
![]() ,
,
∴Rt△DBE≌Rt△DCN(HL)
∴BE=CN,
在Rt△DEA和Rt△DNA中,
![]() ,
,
∴Rt△DEA≌Rt△DNA(HL),
∴AN=AE,
∴BE=AC+AN=AC+AE,
即BE=AE+AC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C= ![]() ,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.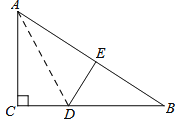
(1)问:△BDE与△BAC相似吗?
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)结合图象写出,0<x<4时,直接写出y的取值范围;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,求出矩形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①) 
阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求间径就是要求⊙O的直径.
(1)再次阅读后,发现AB=寸,CD=寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件.
(2)帮助小智求出⊙O的直径 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
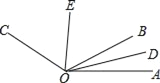
【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的AD边上一个动点,矩形的两条边AB、BC长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )
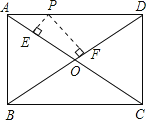
A. 4.8 B. 5 C. 6 D. 7.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com