
【题目】如图,在Rt△ABC中,∠C= ![]() ,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.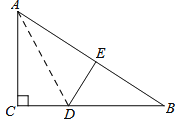
(1)问:△BDE与△BAC相似吗?
(2)已知AC=6,BC=8,求线段AD的长度.
【答案】
(1)
解答:相似.理由如下:
∵∠C= ![]() ,△ACD沿AD折叠,使得点C落在斜边AB上的点E处,
,△ACD沿AD折叠,使得点C落在斜边AB上的点E处,
∴∠C=∠AED= ![]() ,
,
∴∠DEB=∠C= ![]() ,
,
∵∠B=∠B,
∴△BDE∽△BAC;
(2)
解答:由勾股定理,得
AB= ![]() =10.
=10.
由折叠的性质知,AE=AC=6,DE=CD,∠AED=∠C= ![]() .
.
∴BE=AB-AE=10-6=4,
在Rt△BDE中,由勾股定理得,
![]() ,
,
即 ![]() ,
,
解得:CD=3,
在Rt△ACD中,由勾股定理得 ![]()
即 ![]() ,
,
解得:AD=3
【解析】根据折叠的性质得出∠C=∠AED= ![]() ,利用∠DEB=∠C , ∠B=∠B证明三角形相似;先由勾股定理求出AB的长,再由折叠的性质知DE=CD , AE=AC , BE=AB-AE , 在Rt△BDE中运用勾股定理求出DE , 即CD , 最后在Rt△ACD中运用勾股定理得出AD .
,利用∠DEB=∠C , ∠B=∠B证明三角形相似;先由勾股定理求出AB的长,再由折叠的性质知DE=CD , AE=AC , BE=AB-AE , 在Rt△BDE中运用勾股定理求出DE , 即CD , 最后在Rt△ACD中运用勾股定理得出AD .
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在3×3正方形网格中,顶点是网格线的交点的三角形叫做格点三角形,给出下列命题: ①一定存在全等的两个格点三角形
②一定存在相似且不全等的两个格点三角形
③一定存在两个格点三角形是位似图形
④一定存在周长和面积均为无理数的格点三角形
其中真命题的个数是( )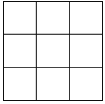
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
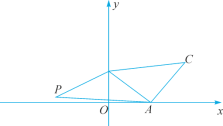
【题目】如图,在平面直角坐标系中,点A(4,0),B(0,3),以线段AB为边在第一象限内作等腰直角三角形ABC,∠BAC=90°.若第二象限内有一点P![]() ,且△ABP的面积与△ABC的面积相等.
,且△ABP的面积与△ABC的面积相等.
(1)求直线AB的函数表达式.
(2)求a的值.
(3)在x轴上是否存在一点M,使△MAC为等腰三角形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y-2与x+1成正比例函数关系,且x=-2时,y=6.
(1)写出y与x之间的函数解析式;
(2)求当x=-3时,y的值;
(3)求当y=4时,x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)将下列各数填在相应的大括号里:
﹣50%,2014,0.61,﹣3,﹣![]() ,0,5.9,﹣3.14,﹣92
,0,5.9,﹣3.14,﹣92
整数:{ ,… }
分数:{ ,… }
负分数:{ ,… }
(2)在(1)的数据中,最大的整数是 ,最小的分数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两商场自行定价销售某一商品.
(1)甲商场将该商品提价15%后的售价为1.15元,则该商品在甲商场的原价为 ▲ 元;
(2)乙商场将该商品提价20%后,用6元钱购买该商品的件数比没提价前少买1件,求该商品在乙商场的原价是多少?
(3)在(1)、(2)小题的条件下,甲、乙两商场把该商品均按原价进行了两次价格调整.
甲商场:第一次提价的百分率是![]() ,第二次提价的百分率是
,第二次提价的百分率是![]() ;
;
乙商场:两次提价的百分率都是![]() (
(![]() .
.
请问甲、乙两商场,哪个商场的提价较多?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列计算过程,发现规律,利用规律猜想并计算:
1+2=![]() =3;1+2+3=
=3;1+2+3=![]() =6,1+2+3+4=
=6,1+2+3+4=![]() =10;1+2+3+4+5=
=10;1+2+3+4+5=![]() =15;…
=15;…
(1)猜想:1+2+3+4+…+n= .
(2)利用上述规律计算:1+2+3+4+…+200;
(3)尝试计算:3+6+9+12+…3n的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC的中垂线DM交∠BAC的平分线AD于D, DE⊥AB于点E,DF⊥AC于F.连接DB、DC
(1)求证:△DBE≌△DFC.
(2)求证:AB+AC=2AE
(3)如图2,若△ABC的边BC的中垂线DM交∠BAC的外角平分线AD于D, DE⊥AB于点E,且AB>AC,写出AE、BE、AC之间的等量关系。(不需证明,只需在图2中作出辅助线、说明证哪两个三角形全等即可)。
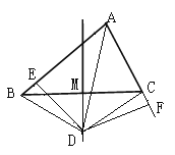
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com