
【题目】如图是2015年12月月历.
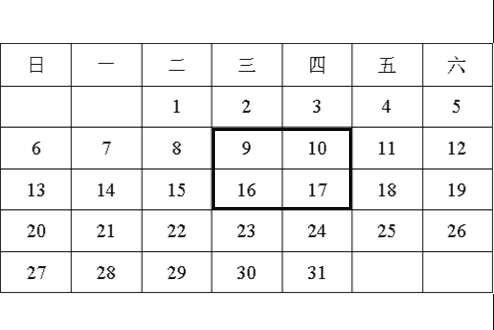
(1)如图,用一正方形框在表中任意框往4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是 , , .
(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2= .
(3)当(1)中被框住的4个数之和等于76时,x的值为多少?
(4)在(1)中能否框住这样的4个数,它们的和等于92?若能,则求出x的值;若不能,则说明理由.
【答案】(1)x+1;x+7;x+8;
(2)128;
(3)当被框住的4个数之和等于76时,x的值为15;
(4)不能.
【解析】解:(1)由图表可知:左右相邻两个数差1,上下相邻的两个数相差为7,左上角的一个数为x,
则另外三个数用含x的式子从小到大依次表示x+1;x+7;x+8;
故答案为x+1;x+7;x+8;
(2)∵当四个数是1,2,8,9时最小,a1=1+2+8+9=20;
当四个数是23,24,30,31时最小,a2=23+24+30+31=108,
∴a1+a2=20+108=128.
故答案为:128;
(3)由题意得,x+x+1+x+7+x+8=76,解得x=15,
答:当被框住的4个数之和等于76时,x的值为15;
(4)不能.
由题意得,x+x+1+x+7+x+8=92,解得x=19,
故由此框住的四个数应是19,20,26,27,但是19,20不在同行的相邻位置,所以不能框住4个数的和等于92.


科目:初中数学 来源: 题型:
【题目】小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
(1)小明距离路灯多远?
(2)求路灯高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
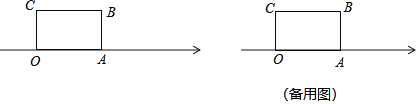
【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)数轴上点A表示的数为几.
(2)将长方形OABC沿OA所在直线水平移动,移动后的长方形记为O′A′B′C′.
①若移动后的长方形O′A′B′C′与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的一半时,求数轴上点A′表示的数.
②若D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,求当长方形OABC移动距离x为何值时,D、E两点到原点O的距离相等?
OO′,求当长方形OABC移动距离x为何值时,D、E两点到原点O的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条街道旁有A,B,C,D,E五幢居民楼,某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:
楼号 | A | B | C | D | E |
大桶水/桶 | 38 | 55 | 50 | 72 | 85 |
他计划在这五幢楼中租赁一间门市房,设立大桶水供应点,若仅考虑这五幢楼内的居民取水所走路程之和最小,则可以选择的地点应在( ).
![]()
A. B楼 B. C楼 C. D楼 D. E楼
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)结合图象写出,0<x<4时,直接写出y的取值范围;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,求出矩形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.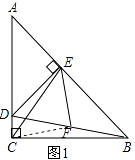
(1)若AD=3 ![]() ,BE=4,求EF的长;
,BE=4,求EF的长;
(2)求证:CE= ![]() EF;
EF;
(3)将图1中的△AED绕点A顺时针旋转,使AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com