
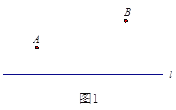
【题目】问题:如图1,点![]() ,
,![]() 在直线
在直线![]() 的同侧,在直线
的同侧,在直线![]() 上找一点
上找一点![]() ,使得
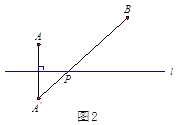
,使得![]() 的值最小.小明的思路是:如图2,作点
的值最小.小明的思路是:如图2,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,则
,则![]() 与直线
与直线![]() 的交点
的交点![]() 即为所求.
即为所求.
请你参考小明同学的思路,探究并解决下列问题:
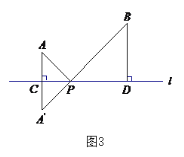
(1)如图3,在图2的基础上,设![]() 与直线
与直线![]() 的交点为
的交点为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() . 若
. 若![]() ,
,![]() ,
,![]() ,写出
,写出![]() 的值为____________;
的值为____________;
(2)将(1)中的条件“![]() ”去掉,换成“
”去掉,换成“![]() ”,其它条件不变,写出此时
”,其它条件不变,写出此时![]() 的值 ___________;
的值 ___________;
(3)求![]() +
+![]() 的最小值.
的最小值.
【答案】 3![]() 5;
5;![]()
【解析】(1)、由勾股定理和相似三角形的性质,求得AP,BP的值即可;(2)、由勾股定理和相似三角形的性质,建立方程求解;(3)、结合图形,由(1)(2)直接写出即可.
(1)、如图2,∵AA′⊥l,AC=1,PC=1,
∴PA=![]() ,∴PA′=PA=
,∴PA′=PA=![]() ,∵AA′∥BD,∴∠A′=∠B,∵∠A′PC=∠BPD,
,∵AA′∥BD,∴∠A′=∠B,∵∠A′PC=∠BPD,
∴△A′PC∽△BPD,∴![]() ,∴
,∴![]() ,∴PB=2
,∴PB=2![]() , ∴AP+PB=
, ∴AP+PB=![]() +2
+2![]() =3
=3![]() ;
;
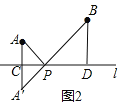
(2)、作AE∥l,交BD的延长线于E,如图3,
则四边形A′EDC是矩形,∴AE=DC=PC+PD=3,DE=A′C=AC,∵BD=4-AC,
∴BD+AC=BD+DE=4,即BE=4,在Rt△A′BE中,A′B=![]() =5,∴AP+BP=5,
=5,∴AP+BP=5,
(3)、如图3,设AC=2m-3,PC=1,则PA=![]() ;设BD=8-2m,PD=2,
;设BD=8-2m,PD=2,
则PB=![]() ,∵DE=AC=2m-3,∴BE=BD+DE=5,A′E=CD=PC+PD=3
,∵DE=AC=2m-3,∴BE=BD+DE=5,A′E=CD=PC+PD=3
∴PA+PB=A′B=![]() .
.



 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
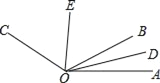
【题目】如图,OD是∠AOB的平分线,OE是∠BOC的平分线.
(1)若∠BOC=50°,∠BOA=80°,求∠DOE的度数;
(2)若∠AOC=150°,求∠DOE的度数;
(3)你发现∠DOE与∠AOC有什么等量关系?给出结论并说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的AD边上一个动点,矩形的两条边AB、BC长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )
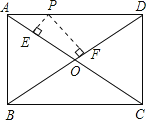
A. 4.8 B. 5 C. 6 D. 7.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗? 若能,求出两段铁丝的长度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到一个问题:AD是△ABC的中线, 点M为BC边上任意一点(不与点D重合),过点M作一直线,使其等分△ABC的面积.
他的做法是:如图1,连结AM,过点D作DN//AM交AC于点N,作直线MN,直线MN即为所求直线.
请你参考小明的做法,解决下列问题:
(1)如图2, AE等分四边形ABCD的面积,M为CD边上一点,过M作一直线MN,使其等分四边形ABCD的面积(要求:在图2中画出直线MN,并保留作图痕迹);
(2)如图3,求作过点A的直线AE,使其等分四边形ABCD的面积(要求:在图3中画出直线AE,并保留作图痕迹).
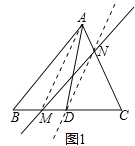

查看答案和解析>>
科目:初中数学 来源: 题型:
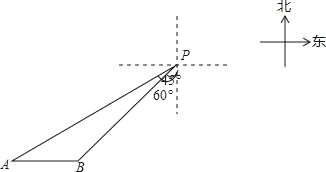
【题目】一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式A=x2+3xy+x-![]() ,B=2x2-xy+4y-1
,B=2x2-xy+4y-1
(1)当x=y=-2时,求2A-B的值;
(2)若2A-B的值与y的取值无关,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
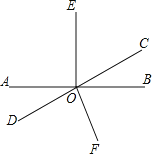
【题目】如图,已知直线AB与直线CD相交于点O,∠BOE=90°,FO平分∠BOD,∠BOC:∠AOC=1:3.
(1)求∠DOE、∠COF的度数.
(2)若射线OF、OE同时绕O点分别以2°/s、4°/s的速度,顺时针匀速旋转,当射线OE、OF的夹角为90°时,两射线同时停止旋转.设旋转时间为t,试求t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE ≌ △CDF,则添加的条件不能为( )
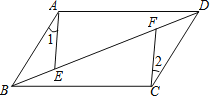
A. BE=DF B. BF=DE C. ∠1=∠2 D. AE=CF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com