
ЎҫМвДҝЎҝФД¶БПВБРІДБПЈә
РЎГчУцөҪТ»ёцОКМвЈәADКЗЎчABCөДЦРПЯЈ¬ өгMОӘBCұЯЙПИОТвТ»өгЈЁІ»УлөгDЦШәПЈ©Ј¬№эөгMЧчТ»ЦұПЯЈ¬К№ЖдөИ·ЦЎчABCөДГж»эЈ®
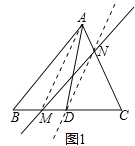
ЛыөДЧц·ЁКЗЈәИзНј1Ј¬Б¬ҪбAMЈ¬№эөгDЧчDN//AMҪ»ACУЪөгNЈ¬ЧчЦұПЯMNЈ¬ЦұПЯMNјҙОӘЛщЗуЦұПЯЈ®
ЗлДгІОҝјРЎГчөДЧц·ЁЈ¬ҪвҫцПВБРОКМвЈә
ЈЁ1Ј©ИзНј2Ј¬ AEөИ·ЦЛДұЯРОABCDөДГж»эЈ¬MОӘCDұЯЙПТ»өгЈ¬№эMЧчТ»ЦұПЯMNЈ¬К№ЖдөИ·ЦЛДұЯРОABCDөДГж»эЈЁТӘЗуЈәФЪНј2ЦР»ӯіцЦұПЯMNЈ¬ІўұЈБфЧчНјәЫјЈЈ©Ј»
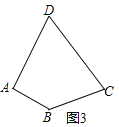
ЈЁ2Ј©ИзНј3Ј¬ЗуЧч№эөгAөДЦұПЯAEЈ¬К№ЖдөИ·ЦЛДұЯРОABCDөДГж»эЈЁТӘЗуЈәФЪНј3ЦР»ӯіцЦұПЯAEЈ¬ІўұЈБфЧчНјәЫјЈЈ©Ј®

Ўҫҙр°ёЎҝјыҪвОц
ЎҫҪвОцЎҝ(1)ЎўБ¬ҪУAMЈ¬№эEЧчENЎОAMЈ¬Ҫ»ADУЪNЈ¬ФЩЧцЦұПЯMNјҙҝЙЈ»(2)ЎўИЎ¶ФҪЗПЯBDөДЦРөгOЈ¬Б¬ҪУAOЎўCOЈ¬ACЈ¬№эөгOЧчOEЎОACҪ»CDУЪEЈ¬ЦұПЯAEҫНКЗЛщЗуЦұПЯЈ®
ЈЁ1Ј©ИзНјЈ®Б¬ҪУAMЈ¬№эEЧчENЎОAMЈ¬Ҫ»ADУЪNЈ¬ФЩЧцЦұПЯMNЈ»
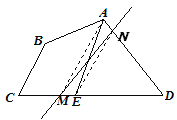
ЈЁ2Ј©ИзНјЈ®ИЎ¶ФҪЗПЯBDөДЦРөгOЈ¬Б¬ҪУAOЎўCOЈ¬ACЈ¬№эөгOЧчOEЎОACҪ»CDУЪEЈ¬ЦұПЯAEҫНКЗЛщЗуЦұПЯЈ®



 ГыРЈҝОМГПөБРҙр°ё
ГыРЈҝОМГПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘkКЗІ»өИУЪ0өДіЈКэЈ¬·ҙұИАэәҜКэУл¶юҙОәҜКэФЪН¬Т»ЧшұкПөөДҙуЦВНјПуИзНјЈ¬ФтЛьГЗөДҪвОцКҪҝЙДЬ·ЦұрКЗЈЁ Ј© 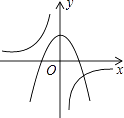
A.y=©Ғ ![]() Ј¬y=©Ғkx2+k
Ј¬y=©Ғkx2+k
B.y= ![]() Ј¬y=©Ғkx2+k
Ј¬y=©Ғkx2+k
C.y= ![]() Ј¬y=kx2+k
Ј¬y=kx2+k
D.y=©Ғ ![]() Ј¬y=©Ғkx2©Ғk
Ј¬y=©Ғkx2©Ғk
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬OОӘЦұПЯABЙПТ»өгЈ¬OCЖҪ·ЦЎПAOEЈ¬ЎПDOE=90ЎгЈ¬ФтТФПВҪбВЫХэИ·өДУР____________Ј®ЈЁЦ»МоРтәЕЈ©
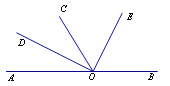
ўЩЎПAODУлЎПBOE»ҘОӘУаҪЗЈ»
ўЪODЖҪ·ЦЎПCOAЈ»
ўЫЎПBOE=56Ўг40ЎдЈ¬ФтЎПCOE=61Ўг40ЎдЈ»
ўЬЎПBOE=2ЎПCODЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
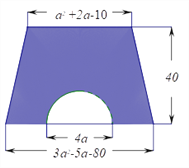
ЎҫМвДҝЎҝИзНјЈ¬МЭРОөДЙПөЧОӘ![]() +2
+2![]() -10Ј¬ПВөЧОӘ3
-10Ј¬ПВөЧОӘ3![]() -5
-5![]() -80Ј¬ёЯОӘ40.ЈЁ
-80Ј¬ёЯОӘ40.ЈЁ![]() ИЎ3Ј©
ИЎ3Ј©
ЈЁ1Ј©УГКҪЧУұнКҫНјЦРТхУ°Іҝ·ЦөДГж»эЈ»
ЈЁ2Ј©өұ![]() =10КұЈ¬ЗуТхУ°Іҝ·ЦГж»эөДЦөЎЈ
=10КұЈ¬ЗуТхУ°Іҝ·ЦГж»эөДЦөЎЈ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝН¬С§ГЗ¶јЦӘөАЈ¬|5©ҒЈЁ©Ғ2Ј©|ұнКҫ5Ул©Ғ2Ц®ІоөДҫш¶ФЦөЈ¬КөјКЙПТІҝЙАнҪвОӘ5Ул©Ғ2БҪКэФЪКэЦбЙПЛщ¶ФөДБҪөгЦ®јдөДҫаАлЈ®КФМҪЛчЈә
ЈЁ1Ј©Зу|5©ҒЈЁ©Ғ2Ј©|=________Ј®
ЈЁ2Ј©КэЦбЙПұнКҫxәН©Ғ1өДБҪөгЦ®јдөДҫаАлұнКҫОӘ________Ј®
ЈЁ3Ј©ХТіцЛщУР·ыәПМхјюөДХыКэxЈ¬К№|x+5|+|x©Ғ2|=7Ј¬ХвСщөДХыКэУР________ёцЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОКМвЈәИзНј1Ј¬өг![]() Ј¬
Ј¬![]() ФЪЦұПЯ
ФЪЦұПЯ![]() өДН¬ІаЈ¬ФЪЦұПЯ
өДН¬ІаЈ¬ФЪЦұПЯ![]() ЙПХТТ»өг
ЙПХТТ»өг![]() Ј¬К№өГ
Ј¬К№өГ![]() өДЦөЧоРЎЈ®РЎГчөДЛјВ·КЗЈәИзНј2Ј¬Ччөг
өДЦөЧоРЎЈ®РЎГчөДЛјВ·КЗЈәИзНј2Ј¬Ччөг![]() №ШУЪЦұПЯ
№ШУЪЦұПЯ![]() өД¶ФіЖөг
өД¶ФіЖөг![]() Ј¬Б¬ҪУ
Ј¬Б¬ҪУ![]() Ј¬Фт
Ј¬Фт![]() УлЦұПЯ
УлЦұПЯ![]() өДҪ»өг
өДҪ»өг![]() јҙОӘЛщЗу.
јҙОӘЛщЗу.
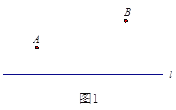
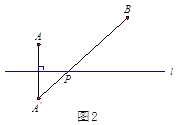
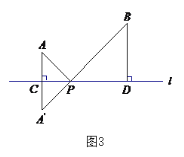
ЗлДгІОҝјРЎГчН¬С§өДЛјВ·Ј¬МҪҫҝІўҪвҫцПВБРОКМвЈә
ЈЁ1Ј©ИзНј3Ј¬ФЪНј2өД»щҙЎЙПЈ¬Йи![]() УлЦұПЯ
УлЦұПЯ![]() өДҪ»өгОӘ
өДҪ»өгОӘ![]() Ј¬№эөг
Ј¬№эөг![]() Чч
Чч![]() Ј¬ҙ№ЧгОӘ
Ј¬ҙ№ЧгОӘ![]() . Иф
. Иф![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬Рҙіц
Ј¬Рҙіц![]() өДЦөОӘ____________Ј»
өДЦөОӘ____________Ј»
ЈЁ2Ј©Ҫ«ЈЁ1Ј©ЦРөДМхјюЎ°![]() ЎұИҘөфЈ¬»»іЙЎ°
ЎұИҘөфЈ¬»»іЙЎ°![]() ЎұЈ¬ЖдЛьМхјюІ»ұдЈ¬РҙіцҙЛКұ
ЎұЈ¬ЖдЛьМхјюІ»ұдЈ¬РҙіцҙЛКұ![]() өДЦө ___________Ј»
өДЦө ___________Ј»
ЈЁ3Ј©Зу![]() +
+![]() өДЧоРЎЦөЈ®
өДЧоРЎЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
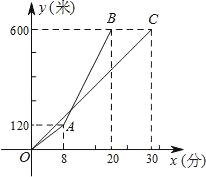
ЎҫМвДҝЎҝјЧЎўТТБҪИЛСШН¬Т»В·ПЯөЗЙҪЈ¬НјЦРПЯ¶ОOCЎўХЫПЯOAB·ЦұрКЗјЧЎўТТБҪИЛөЗЙҪөДВ·іМyЈЁГЧЈ©УлөЗЙҪКұјдxЈЁ·ЦЈ©Ц®јдөДәҜКэНјПуЈ®ЗлёщҫЭНјПуЛщМṩөДРЕПўЈ¬ҪвҙрИзПВОКМвЈә
ЈЁ1Ј©ЗујЧөЗЙҪөДВ·іМУлөЗЙҪКұјдЦ®јдөДәҜКэ№ШПөКҪЈ¬ІўРҙіцЧФұдБҝxөДИЎЦө·¶О§Ј»
ЈЁ2Ј©ЗуТТіц·ўәу¶аіӨКұјдЧ·ЙПјЧЈҝҙЛКұТТЛщЧЯөДВ·іМКЗ¶аЙЩГЧЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ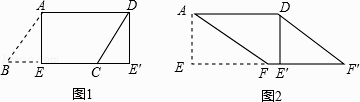
ЈЁ1Ј©ИзНј1ЛщКҫЈ¬ЖҪРРЛДұЯРОЦҪЖ¬ABCDЦРЈ¬AD=5Ј¬SABCD=15Ј¬№эөгAЧчAEЎНBCЈ¬ҙ№ЧгОӘEЈ¬СШAEјфПВЎчABEЈ¬Ҫ«ЛьЖҪТЖЦБЎчDCEЎдөДО»ЦГЈ¬ЖҙіЙЛДұЯРОAEEЎдDЈ¬ФтЛДұЯРОAEEЎдDКЗРОЈ®
ЈЁ2Ј©ИзНј2ЛщКҫЈ¬ФЪЈЁ1Ј©ЦРөДЛДұЯРОЦҪЖ¬AEEЎдDЦРЈ¬ФЪEEЎдЙПИЎТ»өгFЈ¬К№EF=4Ј¬јфПВЎчAEFЈ¬Ҫ«ЛьЖҪТЖЦБЎчDEЎдFЎдөДО»ЦГЈ¬ЖҙіЙЛДұЯРОAFFЎдDЈ®
ўЩЗуЦӨЈәЛДұЯРОAFFЎдDКЗБвРОЈ»
ўЪЗуЛДұЯРОAFFЎдDБҪМх¶ФҪЗПЯөДіӨЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЎчABCЦРЈ¬AB=BCЈ¬DКЗACЦРөгЈ¬BEЖҪ·ЦЎПABDҪ»ACУЪөгEЈ¬өгOКЗABЙПТ»өгЈ¬ЎСO№эBЎўEБҪөгЈ¬Ҫ»BDУЪөгGЈ¬Ҫ»ABУЪөгFЈ® 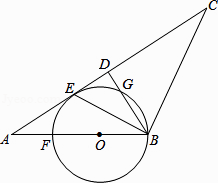
ЈЁ1Ј©ЕР¶ПЦұПЯACУлЎСOөДО»ЦГ№ШПөЈ¬ІўЛөГчАнУЙЈ»
ЈЁ2Ј©өұBD=6Ј¬AB=10КұЈ¬ЗуЎСOөД°лҫ¶Ј®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com