练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，O为直线AB上一点，OC平分∠AOE，∠DOE=90°，则以下结论正确的有____________．（只填序号）

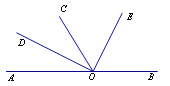
    ①∠AOD与∠BOE互为余角；

    ②OD平分∠COA；

    ③∠BOE=56°40′，则∠COE=61°40′；

    ④∠BOE=2∠COD．

    【答案】①③④

    【解析】试题解析：∵∠DOE=90°，
    ∴∠COD+∠COE=90°，∠EOB+∠DOA=90°，（①正确）

    若∠BOE=56°40′，
    ∵∠AOE+∠BOE=180°，
    ∴∠COE=（180°-∠BOE）=61°40′．（③正确）
    ∵OC平分∠AOE，
    ∴∠AOE=2∠COE=2∠AOC；
    ∵∠BOE=180°-2∠COE，
    ∴∠COD=90°-∠COE
    ∴∠BOE=2∠COD成立.（④正确）

    ∴①③④正确．

    故答案为：①③④.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】《九章算术》是中国传统数学重要的著作，奠定了中国传统数学的基本框架．《九章算术》中记载：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，间径几何？”（如图①）
    阅读完这段文字后，小智画出了一个圆柱截面示意图（如图②），其中BO⊥CD于点A，求间径就是要求⊙O的直径．
    （1）再次阅读后，发现AB=寸，CD=寸（一尺等于十寸），通过运用有关知识即可解决这个问题．请你补全题目条件．
    （2）帮助小智求出⊙O的直径 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，OC在∠BOD内．

    （1）如果∠AOC和∠BOD都是直角．

    ①若∠BOC=60°，则∠AOD的度数是　 　；

    ②猜想∠BOC与∠AOD的数量关系，并说明理由；

    （2）如果∠AOC=∠BOD=x°，∠AOD=y°，求∠BOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个袋子中装有3个红球和2个黄球，这些球的形状、大小．质地完全相同，在看不到球的条件下，随机从袋子里同时摸出2个球，其中2个球的颜色相同的概率是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙的直径，CD是∠ACB的平分线交⊙O于点D，过D作⊙O的切线交CB的延长线于点E．若AB=4，∠E=75°，则CD的长为（ ）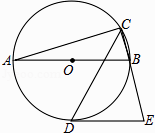
    A.
    B.2
    C.2
    D.3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，P是矩形ABCD的AD边上一个动点，矩形的两条边AB、BC长分别是6和8，则点P到矩形的两条对角线距离之和PE+PF是（ ）

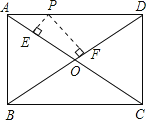
    A. 4.8 B. 5 C. 6 D. 7.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．
    （1）求直线AB的解析式；
    （2）若直线AB上的点C在第一象限，且S△BOC=2，求经过点C的反比例函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

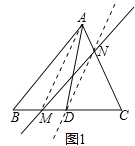
    【题目】阅读下列材料：

    小明遇到一个问题：AD是△ABC的中线， 点M为BC边上任意一点（不与点D重合），过点M作一直线，使其等分△ABC的面积．

    他的做法是：如图1，连结AM，过点D作DN//AM交AC于点N，作直线MN，直线MN即为所求直线．

    请你参考小明的做法，解决下列问题：

    （1）如图2， AE等分四边形ABCD的面积，M为CD边上一点，过M作一直线MN，使其等分四边形ABCD的面积（要求：在图2中画出直线MN，并保留作图痕迹）；

    （2）如图3，求作过点A的直线AE，使其等分四边形ABCD的面积（要求：在图3中画出直线AE，并保留作图痕迹）．

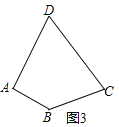
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明同学骑自行车去郊外春游，骑行1小时后，自行车出现故障，维修好后继续骑行，下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的图象．

    (1)根据图象回答：小明到达离家最远的地方用了多长时间？此时离家多远？

    (2)求小明出发2.5小时后离家多远；

    (3)求小明出发多长时间离家12千米．

    查看答案和解析>>

    同步练习册答案