
【题目】如图,梯形的上底为![]() +2
+2![]() -10,下底为3
-10,下底为3![]() -5
-5![]() -80,高为40.(
-80,高为40.(![]() 取3)
取3)
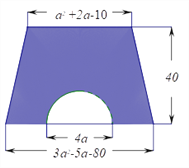
(1)用式子表示图中阴影部分的面积;
(2)当![]() =10时,求阴影部分面积的值。
=10时,求阴影部分面积的值。
【答案】(1)、74a2﹣60a﹣1800;(2)、5000.
【解析】试题分析:(1)、阴影部分的面积=梯形的面积-半圆的面积,然后用代数式进行表示出来,然后进行合并同类项化简;(2)、将a的值代入化简后的式子进行计算.
试题解析:(1)、∵梯形的上底为a2+2a﹣10,下底为3a2﹣5a﹣80,高为40,半圆的直径为4a,
∴阴影部分的面积=![]() (a2+2a﹣10+3a2﹣5a﹣80)×40﹣
(a2+2a﹣10+3a2﹣5a﹣80)×40﹣![]() π(
π(![]() )2,
)2,
=80a2﹣60a﹣1800﹣2a2π,
=80a2﹣60a﹣1800﹣2a2×3,
=74a2﹣60a﹣1800;
(2)、当a=10时,74a2﹣60a﹣1800=74×102﹣60×10﹣1800=5000.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一个袋子中装有3个红球和2个黄球,这些球的形状、大小.质地完全相同,在看不到球的条件下,随机从袋子里同时摸出2个球,其中2个球的颜色相同的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的AD边上一个动点,矩形的两条边AB、BC长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )
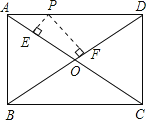
A. 4.8 B. 5 C. 6 D. 7.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2). 
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求经过点C的反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗? 若能,求出两段铁丝的长度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
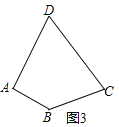
小明遇到一个问题:AD是△ABC的中线, 点M为BC边上任意一点(不与点D重合),过点M作一直线,使其等分△ABC的面积.
他的做法是:如图1,连结AM,过点D作DN//AM交AC于点N,作直线MN,直线MN即为所求直线.
请你参考小明的做法,解决下列问题:
(1)如图2, AE等分四边形ABCD的面积,M为CD边上一点,过M作一直线MN,使其等分四边形ABCD的面积(要求:在图2中画出直线MN,并保留作图痕迹);
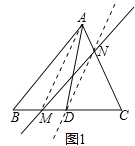
(2)如图3,求作过点A的直线AE,使其等分四边形ABCD的面积(要求:在图3中画出直线AE,并保留作图痕迹).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式A=x2+3xy+x-![]() ,B=2x2-xy+4y-1
,B=2x2-xy+4y-1
(1)当x=y=-2时,求2A-B的值;
(2)若2A-B的值与y的取值无关,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上. 
(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com