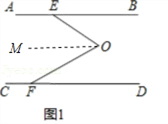
试题分析:(1)证明:过O作OM∥AB,
∵AB∥CD,
∴AB∥OM∥CD,
∴∠BEO=∠MOE,∠DFO=∠MOF,
∴∠BEO+∠DFO=∠EOM+∠FOM,
即∠EOF=∠BEO+∠DFO.
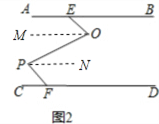
(2)满足的关系式是:∠BEO+∠P=∠O+∠PFC,
解:过O作OM∥AB,PN∥AB,
∵AB∥CD,
∴AB∥OM∥PN∥CD,
∴∠BEO=∠EOM,∠PFC=∠NPF,∠MOP=∠NPO,
∴∠EOP﹣∠OPF=(∠EOM+∠MOP)﹣(∠OPN+∠NPF)=∠EOM﹣∠NPF,
∠BEO﹣∠PFC=∠EOM﹣∠NPF,
∴∠BEO﹣∠PFC=∠EOP﹣∠OPF,
∴∠BEO+OPF=∠EOP+∠PFC.
(3)解:如果两平行线间存在一条折线,则所有同向角的和相等。
或者:向左凸出的角的和等于向右面凸出的角的和
点评:本题难度较大,主要考查学生对平行线性质与判定的运用,为中考几何问题中常见题型,学生要牢固掌握。注意培养数形结合的思想,并运用到实际考试中。



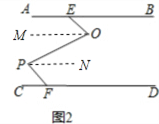


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案