练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    6.如图，D、E、F分别是等边△ABC三个边上的点，且AD=BE=CF．

    求证：△DEF是等边三角形．

    分析：根据等边△ABC中AD=BE=CF，证得△ADF≌△BED≌△CFE即可得出：△DEF是等边三角形．

    解答：证明：∵△ABC为等边三角形，且AD=BE=CF
    ∴AF=BD=CE，
    又∵∠A=∠B=∠C=60°，
    ∴△ADF≌△BED≌△CFE（SAS），
    ∴DF=ED=EF，
    ∴△DEF是一个等边三角形．

    点评：此题主要考查了等边三角形的判定与性质和全等三角形判定，根据已知得出△ADF≌△BED≌△CFE是解题关键．

    题目来源：初中同步测控优化设计八年级数学上册人教版 > 13.3.2等边三角形

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    10、若n是正整数，且x^n=6,y^n=6=5,求（xy）^2n的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    5、如果长方体的长为（3a-4),宽为2a,高为a,则它的体积为（）

    A、1/2（3a-4).2a.a=3a^3-4a^2

    B、1/2a.2a=a^2

    C、（3a-4).2a.a=6a^3-8a^2

    D、2a.（3a-4)=6^2-8a

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    6.实数a，b，c在数轴上的对应点如图所示，a+|a+b|-|b-c|-|b+c-a|=__________.

                                                                     


                                                                 

     

                                                                     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

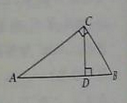
    6.如图，在△ABC中，∠ACB=90°，∠A=30°，CD⊥AB，AB=4。则BC=_______，∠BCD=_______，BD=__________.                           

                                                                  

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    9.如图，D、E分别是等边三角形ABC两边BC、AC上的点，且AE=CD，连结AD、BE交于点P，过点B作BQ⊥AD于点Q。 请说明BP=2PQ

                                            。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    4.等边△ABC中，点D、E分别是边AB、AC的中点，CD、BE交于点O，则∠BOC的度数是（    ）．

    A.90°    B.100°     C.120°      D.150°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    (a-2b)(        )=-[(2b)^2-a^2]

    查看答案和解析>>

    同步练习册答案