
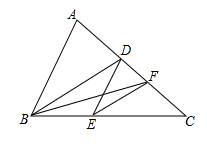
9.如图,D、E分别是等边三角形ABC两边BC、AC上的点,且AE=CD,连结AD、BE交于点P,过点B作BQ⊥AD于点Q。 请说明BP=2PQ
。
证明:在△BAE和△ACD中。
∵△ABC是等边三角形 ∴∠BAE=∠ACD=60°
AB=AE
AE=CD(已知)
∴△BAE≌△ACD(S.A.S)
则:∠ABE=∠CAD ∵∠BAC=∠BAP+∠CAD=60°
∴∠BAP+∠ABP=60°
那么:∠BPQ=∠BAP+∠ABP=60°(三角形的一个外角等于与它不相邻的两个内角和。
∵BQ⊥AD
∴∠BQP=90°
则:∠PBQ=180°-∠BQP-∠BPQ=180°-90°-60°=30°;
∴PQ=1/2BP(直角三角形中,30°所对应的直角边等于斜边的一半。)
题目来源:初中同步测控优化设计八年级数学上册人教版 > 13.3.2等边三角形


科目:初中数学 来源: 题型:
19.找规律,按如图所示的方法摆下去。
(1)第一个中有几个正方体?第2个中有几个正方体?第3个中有几个正方体?
(2)第5个中有几个正方体?第10个中有几个正方体?第n个中有几个正方体?

查看答案和解析>>
科目:初中数学 来源: 题型:
下列运算中,运算结果正确的是()
A、(-6x)(2x-3y)=-12x^2-18xy
B、5x(3x^2-2x+3)=15x^3-10x^2+3
C、4ab[2a^2b-3b(ab-ab^2)]=8a^3b^2-12ab^2(4a^2b^2-4a^2b^3)
D、a(a+b)-b(a+b)=a^2-b^2
查看答案和解析>>
科目:初中数学 来源: 题型:
新课早知
1.三条边都______的三角形叫做等边三角形。
2.等边三角形的________________,并且每一个角都等于60°。
3.__________________的三角形是等边三角形。______________________的等腰三角形是等边三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com