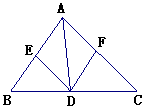
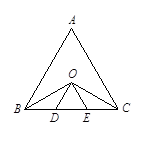试题分析:(1)直观上看△ODE是等边三角形,要证明一个三角形是等边三角形,要么证明三边相等,或者有两个角是60°或者有一个角是60°的等腰三角形,由题,在等边△ABC中,AB=AC=BC,∠ABC=∠ACB=60°,又∵OD∥AB,所以∠ABC=∠ODE=60°,同理, ∵OE∥AC,所以∠ACB=∠OED=60°,所以△ODE是等边三角形;(2)直观上看BD=DE=EC,∵∠ABC与∠ACB的平分线相交于点O,所以∠ABO=∠OBD,∠ACO=∠OCD,又∵OD∥AB,所以∠OBD=∠ABO=∠BOD.所以BD=OD,∵OE∥AC,所以∠ACO=∠OCD =∠COE,所以CE=OE,由(1)知△ODE是等边三角形,所以OD=DE=OE,即BD=DE=EC.
试题解析:(1)由题,在等边△ABC中,AB=AC=BC,∠ABC=∠ACB=60°,
又∵OD∥AB,
∴∠ABC=∠ODE=60°,
同理, ∵OE∥AC,
∴∠ACB=∠OED=60°,
∴△ODE是等边三角形.
(2)∵∠ABC与∠ACB的平分线相交于点O,
∴∠ABO=∠OBD,∠ACO=∠OCD,
又∵OD∥AB,
∴∠OBD=∠ABO=∠BOD.
∴BD=OD,
∵OE∥AC,
∴∠ACO=∠OCD =∠COE,
∴CE=OE,
由(1)知△ODE是等边三角形,
∴OD=DE=OE,即BD=DE=EC.