
【题目】如图①,矩形ABCD的对角线AC,BD交于点O,过点D作DP∥OC,且DP=OC,连接CP.
(1)判断四边形CODP的形状并说明理由;
(2)如图②,如果题目中的矩形变为菱形,判断四边形CODP的形状并说明理由;
(3)如图③,如果题目中的矩形变为正方形,判断四边形CODP的形状并说明理由.
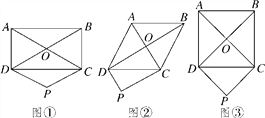
【答案】(1)四边形CODP是菱形,理由见解析; (2)四边形CODP是矩形,理由见解析;(3)四边形CODP是正方形,理由见解析.
【解析】试题分析:(1)根据矩形的性质得出OD=OC,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据菱形的判定推出即可;
(2)根据菱形的性质得出∠DOC=90°,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据矩形的判定推出即可;
(3)根据正方形的性质得出OD=OC,∠DOC=90°,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据正方形的判定推出即可;
试题解析:
(1)四边形CODP的形状是菱形,理由是:
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,
BD,
∴OC=OD,
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵OC=OD,
∴平行四边形CODP是菱形;
(2)四边形CODP的形状是矩形,
理由是:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵∠DOC=90°,
∴平行四边形CODP是矩形;
(3)四边形CODP的形状是正方形,
理由是:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,
BD,
∴∠DOC=90°,OD=OC,
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵∠DOC=90°,OD=OC
∴平行四边形CODP是正方形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)来表示.例如f(x)=x2+3x-5,把x=某数时多项式的值用f(某数)来表示.例如x=-1时多项式x2+3x-5的值记为f(-1)=(-1)2+3×(-1)-5=-7.
(1)已知g(x)=-2x2-3x+1,分别求出g(-1)和g(-2);
(2)已知h(x)=ax3+2x2-ax-6,当h(![]() )=a,求a的值;
)=a,求a的值;
(3)已知f(x)=![]() -
-![]() -2(a,b为常数),当k无论为何值,总有f(1)=0,求a,b的值.
-2(a,b为常数),当k无论为何值,总有f(1)=0,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1)a=______________,b=_____________,点B的坐标为_______________;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )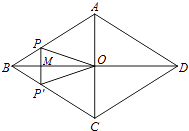
A.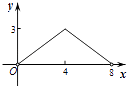
B.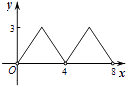
C.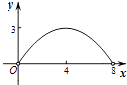
D.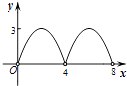
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD∥EF,∠1=75,∠2=45,点 G为∠BED 内一点,且 EG把∠BED分成 1 ∶ 2 两部分,则∠GEF 的度数为 ___.
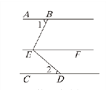
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空完成推理过程:
如图,AD⊥BC于点D,EG⊥BC于点G,AD平分∠BA C. 求证: ∠E=∠1.
证明: ∵AD⊥BC于点D,EG⊥BC于点G,(已知)
∴∠ADC=∠EGC=90°,(垂直的定义)
∴AD∥EG,( )
∴∠1= ,( )
∠E=∠3,(两直线平行,同位角相等)
∵AD平分∠BAC,(已知)
∴∠2=∠3,( )
∴∠E=∠1.(等量代换)
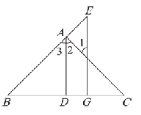
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上的一点,OC为任一射线,OD平分∠BOC,OE平分∠AOC.
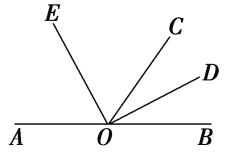
(1)指出图中∠AOD的补角和∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式计算正确的是( )
A. 7-2×(-![]() )=5×(-
)=5×(-![]() )=-1 B. -3÷7×
)=-1 B. -3÷7×![]() =-3÷1=-3
=-3÷1=-3
C. -32-(-3)2=-9-9=-18 D. 3×23-2×9=3×6-18=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s). 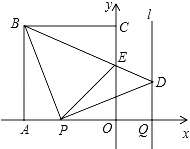
(1)∠PBD的度数为 , 点D的坐标为(用t表示);
(2)当t为何值时,△PBE为等腰三角形?
(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com