
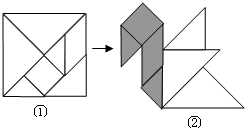
 用正方形纸板制成一副七巧板,如图①,将它拼成“小天鹅”图案,如图②,若其中阴影部分的面积为6,则正方形纸板的面积为( )
用正方形纸板制成一副七巧板,如图①,将它拼成“小天鹅”图案,如图②,若其中阴影部分的面积为6,则正方形纸板的面积为( )| A. | 12 | B. | 16 | C. | 18 | D. | 25 |
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 6 | 4 | 2 | 0 | -2 | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
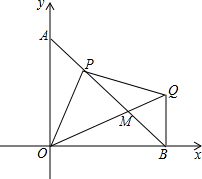 已知:如图,A、B两点坐标为(0,4),B(4,0),P为线段AB上的任一点,过P作OP的垂线与过B点的x轴的垂线交于点Q,OQ与直线AB交于点M.请探究解答下列问题:
已知:如图,A、B两点坐标为(0,4),B(4,0),P为线段AB上的任一点,过P作OP的垂线与过B点的x轴的垂线交于点Q,OQ与直线AB交于点M.请探究解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某城区为了改善全区中、小学办学条件,去年分三批为学校配备了教学器材,其中第三批共投入经费144000元.采购了电子白板16块和投影机8台.已知1块电子白板的单价比1台投影机的多3000元.
某城区为了改善全区中、小学办学条件,去年分三批为学校配备了教学器材,其中第三批共投入经费144000元.采购了电子白板16块和投影机8台.已知1块电子白板的单价比1台投影机的多3000元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com