（本小题满分8分）
使得函数值为零的自变量的值称为函数的零点．例如，对于函数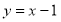
，令
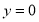，可得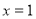
，我们就说1是函数
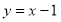的零点．
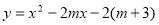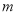已知函数
（
为常数）．
（1）当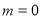
时，求该函数的零点；
（2）证明：无论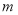
取何值，该函数总有两个零点．
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案科目：初中数学 来源：2014-2015学年山东省九年级中考第三次模拟数学试卷（解析版） 题型：解答题
【课本节选】
反比例函数y= （k为常数,k≠0）的图象是双曲线.当k＞0时，双曲线两个分支分别在三象限,在每一个象限内,y随x的增大而减小（简称增减性）；反比例函数的图象关于原点对称（简称对称性）．这些我们熟悉的性质，可以通过说理得到吗？
【尝试说理】
我们首先对反比例函数y=（k＞0）的增减性来进行说理．如图，当x＞0时．
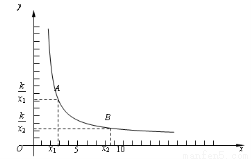
在函数图象上任意取两点A、B，设A（x1，），B（x2，），
且0＜x1＜ x2．
下面只需要比较和的大小．
—= ．
∵0＜x1＜ x2，∴x1－x2＜0，x1 x2＞0，且 k＞0．
∴＜0．即＜ ．
这说明：x1＜ x2时，＞．也就是：自变量值增大了，对应的函数值反而变小了．
即：当x＞0时，y随x的增大而减小．
同理，当x＜0时，y随x的增大而减小．
（1）试说明：反比例函数y= （k＞0）的图象关于原点对称．
【运用推广】
（2）分别写出二次函数y=ax2 （a＞0，a为常数）的对称性和增减性，并进行说理．
对称性： ；
增减性： ．
说理：
（3）对于二次函数y=ax2＋bx＋c （a＞0，a，b，c为常数），请你从增减性的角度，简要解释为何当x=— 时函数取得最小值．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省九年级中考第三次模拟数学试卷（解析版） 题型：选择题
对参加某次野外训练的中学生的年龄（单位：岁）进行统计，结果如下：
年龄 | 14 | 15 | 16 | 17 | 18 |
人数 | 5 | 6 | 6 | 7 | 2 |
则这些学生年龄的众数和中位数分别是
A．17 15．5 B．17 16 C．15 15．5 D．16 16
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省九年级学业水平5月模拟考数学试卷（解析版） 题型：填空题
（本小题满分7分）
学校为了解全校l 600名学生到校上学的方式，在全校随机抽取了若干名学生进行问卷调查．问卷给出五种上学方式供学生选择，每人只能选一项，且不能不选．将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图（均不完整）．（直接填写答案）
（1）在这次调查中，一共要抽取学生__________名；
（2）在这次调查中，抽取的学生中步行有__________名；
（3）估计全校所有乘坐公交车上学的学生__________人．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省九年级学业水平5月模拟考数学试卷（解析版） 题型：填空题
PM2．5是指大气中直径小于或等于2．5微米的颗粒物，2．5微米等于0．000 0025米，把0．000 0025用科学记数法表示为__________．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省陵县九年级学业水平考试数学试卷（解析版） 题型：填空题
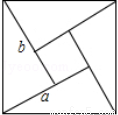
如图，我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形，若小正方形与大正方形的面积之比为1：13，则直角三角形较短的直角边a与较长的直角边b的比值为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的图象经过点P（
，
）和Q（
，
），则
的值为________．
B．
C．
D．