
【题目】如图1,AB∥CD,∠BAD,∠ADC 的平分线AE,DE相交于点E.
(1)证明:AE⊥DE;
(2)如图2,过点E作直线AB,AD,DC的垂线,垂足分别为F,G,H,证明:EF=EG=EH;
(3)如图3,过点E的直线与AB,DC分别相交于点B,C(B、C在AD的同侧)
①求证: E为线段BC的中点;
②若S△ADE=8, S△ABE=2,求△CDE的面积.

【答案】(1)见详解;(2)见详解;(3)①见详解;②6
【解析】
(1)由AB∥CD,可知![]() ,再由角平分线的定义可得
,再由角平分线的定义可得![]() ,由三角形内角和可得
,由三角形内角和可得![]() ,则结论可证;
,则结论可证;
(2)由角平分线的性质即可证明EF=EG=EH;
(3)①过点E作EF⊥AB交AB的延长线于点F,EG⊥CD交CD于点G,由第(2)问中可知EF=EG,则可利用ASA证明![]() ,则
,则![]() ,则结论可证;
,则结论可证;
②通过计算可知![]() ,则△CDE的面积可求.
,则△CDE的面积可求.
(1)证明:∵AB∥CD
∴![]()
∵AE平分![]() ,DE平分
,DE平分![]() ,
,
∴![]()
∴![]()
∴![]()
∴AE⊥DE
(2)∵AE平分![]() ,
,![]()
∴![]()
∵DE平分![]() ,
,![]()
∴![]()
∴![]()
(3)①过点E作EF⊥AB交AB的延长线于点F,EG⊥CD交CD于点G,
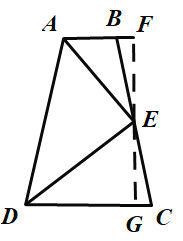
由(2)可知![]()
∵EF⊥AB,EG⊥CD
∴![]()
在![]() 和
和![]() 中,
中,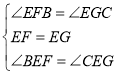
∴![]()
∴![]()
∴E为线段BC的中点
②∵![]()
∴![]()
∵![]()
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】(12分)如图,经过点C(0,﹣4)的抛物线![]() (
(![]() )与x轴相交于A(﹣2,0),B两点.
)与x轴相交于A(﹣2,0),B两点.

(1)a 0,![]() 0(填“>”或“<”);
0(填“>”或“<”);
(2)若该抛物线关于直线x=2对称,求抛物线的函数表达式;
(3)在(2)的条件下,连接AC,E是抛物线上一动点,过点E作AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点所组成的四边形是平行四边形?若存在,求出满足条件的点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF、EF相交于点F.

(1)求证:∠C=∠BAD;
(2)求证:AC=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
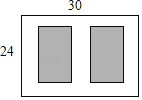
【题目】如图,某小区有一块长为30 m,宽为24 m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为________m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AD=5cm, AP=8cm , AP平分∠DAB,交DC于点P,过点B作BE⊥AD于点E,BE交AP于点F,则tan∠BFP= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,小明拿着老师的等腰直角三角尺玩,不小心掉到两堆砖块之间,如图所示.

(1)求证:△ADC≌△CEB;
(2)已知DE=35cm,请你帮小明求出砖块的厚度a的大小(每块砖的厚度相同).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx﹣3的图象与x轴交于B,C两点(点B在点C的左侧),一次函数y=mx+n的图象经过点B(﹣2,0)和二次函数图象上另一点A(4,3),若点M在直线AB上,且与点A的距离是它到x轴的距离的![]() 倍,则点M的坐标_____.
倍,则点M的坐标_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com