练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在运动会径赛中，甲、乙同时起跑，刚跑出200m，甲不慎摔倒，他又迅速地爬起来继续投入比赛，若他们所跑的路程y（m）与比赛时间x（s）的关系如图，有下列说法：①他们进行的是800m比赛；②乙全程的平均速度为6.4m/s；③甲摔倒之前，乙的速度快；④甲再次投入比赛后的平均速度为7.5m/s；⑤甲再次投入比赛后在距离终点300米时追上了乙．其中正确的个数有（　　）

    A.2个B.3个C.4个D.5个

    【答案】B

    【解析】

    ①由函数图象可以直接得出比赛的距离；

    ②由路程÷时间就可以得出速度得出结论；

    ③由函数图象可以得出相同的时间乙走的路程少，所以乙的速度慢；

    ④由600÷80就可以求出甲再次投入比赛后的平均速度而得出结论；

    ⑤由待定系数法分别求出BC和OD的解析式就可以求出结论．

    ①由函数图象，得：甲乙比赛的距离为800米，故正确；

    ②题意，得800÷125=6.4m/s，故正确；

    ③由函数图象，得

    甲摔倒之前，甲的速度快．故错误；

    ④由题意，得600÷80=7.5m/s，故正确；

    ⑤设BC的解析式为y=kx+b，OD的解析式为y=k1x，由题意，得

    解得：，k1=6.4，

    ∴y=7.5x-100，y=6.4x，

    7.5x-100=6.4x，

    解得：x=．

    800-6.4×=≠300，故错误．

    综上所述，正确的有3个．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】操作发现：如图，已知△ABC和△ADE均为等腰三角形，AB＝AC，AD＝AE，将这两个三角形放置在一起，使点B，D，E在同一直线上，连接CE．

    （1）如图1，若∠ABC＝∠ACB＝∠ADE＝∠AED＝55°，求证：△BAD≌△CAE；

    （2）在（1）的条件下，求∠BEC的度数；

    拓广探索：（3）如图2，若∠CAB＝∠EAD＝120°，BD＝4，CF为△BCE中BE边上的高，请直接写出EF的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=k1x+b与反比例函数y=的图象交于第一象限内的P（，8），Q（4，m）两点，与x轴交于A点．

    （1）分别求出这两个函数的表达式；

    （2）写出点P关于原点的对称点P'的坐标；

    （3）求∠P'AO的正弦值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】张老师给爱好学习的小军和小俊提出这样一个问题：如图①，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．

    小军的证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．

    小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．

    【变式探究】如图③，当点P在BC延长线上时，其余条件不变，求证：PD﹣PE=CF；请运用上述解答中所积累的经验和方法完成下题：

    【结论运用】如图④，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=8，CF=3，求PG+PH的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）操作发现：

    在△ABC中，AB=AC，∠BAC=90°，D在线段BC上（不与点B重合），连接AD，将线段AD绕A点逆时针旋转90°得到AE，连接EC，如图①所示，请直接写出线段CE和BD的位置关系和数量关系．

    （2）猜想论证：

    在（1）的条件下，当D在线段BC的延长线上时，请你在图②中画出图形并判断（1）中的结论是否成立，并证明你的判断．

    （3）拓展延伸：

    如图③，若AB≠AC，∠BAC≠90°，点D在线段BC上运动，试探究：当锐角∠ACB等于　 　度时，线段CE和BD之间的位置关系仍成立（点C、E重合除外）？此时若作DF⊥AD交线段CE于点F，且当AC=3时，请直接写出线段CF的长的最大值是　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

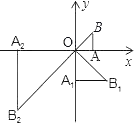
    【题目】如图，在平面直角坐标系xoy中，有一个等腰直角三角形AOB，∠OAB=90°，直角边AO在x轴上，且AO=1．将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O=2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2，且A2O=2A1O，…，依此规律，得到等腰直角三角形A2018OB2018，则点A2018的坐标为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，，分别是，上的动点，将沿折叠.

    (1)当点与点重合时，如图1.若，，则的周长为_____.

    (2)定义：若在三角形中，期中一条边是另一条边的2倍，则称这个三角形为“倍边三角形”.当点与点重合时，如图2.若，则是倍边三角形吗？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设y是关于x的一次函数，其图象与y轴交点的纵坐标为﹣10，且当x＝1时，y＝﹣5．

    （1）求该一次函数图象与坐标轴围成的三角形面积；

    （2）当函数值为时，自变量的取值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两个大小不同的等腰直角三角形三角板如图 1 所示放置，图 2 是由它抽像出的几何图形，B, C, E在同一 条直线上，连结DC.

    (1)请找出图 2 中的全等三角形，并给予证明(说明:结论中不得含有未标识的字 母);

    (2)证明:DC ⊥ BE.

    查看答案和解析>>

    同步练习册答案