
【题目】设y是关于x的一次函数,其图象与y轴交点的纵坐标为﹣10,且当x=1时,y=﹣5.
(1)求该一次函数图象与坐标轴围成的三角形面积;
(2)当函数值为![]() 时,自变量的取值是多少?
时,自变量的取值是多少?
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】在运动会径赛中,甲、乙同时起跑,刚跑出200m,甲不慎摔倒,他又迅速地爬起来继续投入比赛,若他们所跑的路程y(m)与比赛时间x(s)的关系如图,有下列说法:①他们进行的是800m比赛;②乙全程的平均速度为6.4m/s;③甲摔倒之前,乙的速度快;④甲再次投入比赛后的平均速度为7.5m/s;⑤甲再次投入比赛后在距离终点300米时追上了乙.其中正确的个数有( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海尔专卖店春节期间,销售10台Ⅰ型号洗衣机和20台Ⅱ型号洗衣机的利润为4000元,销售20台Ⅰ型号洗衣机和10台Ⅱ型号洗衣机的利润为3500元.
(1)求每台Ⅰ型号洗衣机和Ⅱ型号洗衣机的销售利润;
(2)该商店计划一次购进两种型号的洗衣机共100台,其中Ⅱ型号洗衣机的进货量不超过Ⅰ型号洗衣机的进货量的2倍,问当购进Ⅰ型号洗衣机多少台时,销售这100台洗衣机的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为斜边的Rt△ABC的每条边为边作三个正方形,分别是正方形ABMN,正方形BCPQ,正方形ACEF,且边EF恰好经过点N.若S3=S4=6,则S1+S5=_____.(注:图中所示面积S表示相应封闭区域的面积,如S3表示△ABC的面积)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地开往B地,甲车比乙车早出发2小时,并且在途中休息了0.5小时,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.解答下列问题:

(1)图中a的值为;
(2)当x>1.5(h)时,求甲车行驶路程y(km)与时间x(h)的函数关系式;
(3)当甲车行驶多长时间后,两车恰好相距40km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“金山”超市现有甲、乙两种糖果若干kg,两种糖果的售价和进价如表
糖果 | 甲种 | 乙种 |
售价 | 36元/kg | 20元/kg |
进价 | 30元/kg | 16元/kg |
(1)超市准备用甲、乙两种糖果混合成杂拌糖出售,混合后糖果的售价是27.2元/kg,现要配制这种杂拌糖果100/kg,需要甲、乙两种糖果各多少千克?
(2)“六一”儿童节前夕,超市准备用5000元购进甲、乙两种糖果共200kg,如何进货才能使这批糖果获得最大利润,最大利润是多少?(注:进货量只能为整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
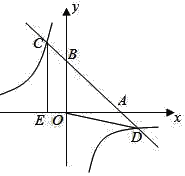
【题目】如图,直角坐标系xOy中,直线y=﹣x+b分别交x,y轴的正半轴于点A,B,交反比例函数y=﹣![]() 的图象于点C,D(点C在第二象限内),过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若
的图象于点C,D(点C在第二象限内),过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若![]() ,则CD的长为____.
,则CD的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com