
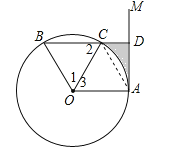
【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若DC=2,求图中阴影部分的面积.(结果保留π和根号)

【答案】(1)答案见解析;(2)![]() .
.
【解析】试题分析:(1)由已知条件得到△BOC是等边三角形,根据等边三角形的性质得到∠1=∠2=60°,由角平分线的性质得到∠1=∠3,根据平行线的性质得到∠OAM=90°,于是得到结论;
(2)根据等边三角形的性质得到∠OAC=60°,根据三角形的内角和得到∠CAD=30°,根据勾股定理得到AD的长,于是得到结论.
(1)∵∠B=60°,∴△BOC是等边三角形,∴∠1=∠2=60°,∵OC平分∠AOB,∴∠1=∠3,∴∠2=∠3,∴OA∥BD,∴∠BDM=90°,∴∠OAM=90°,∴AM是⊙O的切线;
(2)∵∠3=60°,OA=OC,∴△AOC是等边三角形,∴∠OAC=60°,∵∠OAM=90°,∴∠CAD=30°,∵CD=2,∴AC=2CD=4,∴AD=![]() ,∴S阴影=S梯形OADC﹣S扇形OAC=
,∴S阴影=S梯形OADC﹣S扇形OAC=![]() (4+2)×
(4+2)×![]() ﹣
﹣![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】核桃和枣是我省著名的农特产,它们营养丰富,有益人体健康,深受老百姓喜爱。某超市从农贸批发市场批发核桃和枣进行零售,批发价和零售价格如下表所示:
名称 | 核桃 | 枣 |
批发价(元/ | 12 | 9 |
零售价(元/ | 18 | 12 |
请解答下列问题.
(1)第一天,该超市从批发市场批发核桃和枣共350![]() ,用去了3600元钱,求当天核桃和枣各批发多少kg?
,用去了3600元钱,求当天核桃和枣各批发多少kg?
(2)第二天,该超市用3600元钱仍然批发核桃和枣(批发价和零售价不变),要想将第二天批发的核桃和枣全部售完后,所获利润不低于40%,则该超市第二天至少批发核桃多少kg?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人承包了一池塘养鱼,他想估计一下收入情况.于是让他上初三的儿子帮忙.他儿子先让他从鱼塘里随意打捞上了60条鱼,把每条鱼都作上标记,放回鱼塘;过了2天,他让他父亲从鱼塘内打捞上了50条鱼,结果里面有2条带标记的.假设当时这种鱼的市面价为2.8元/斤,平均每条鱼估计2.3斤,你能帮助他估计一下今年的收入情况吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为原点,数轴上两点A、B所对应的数分别为m、n,且m、n满足关于x、y的整式x41+myn+60与2xy3n之和是单项式,动点P以每秒4个单位长度的速度从点A向终点B运动.
(1)求m、n的值;
(2)当PB-(PA+PO)=10时,求点P的运动时间t的值;
(3)当点P开始运动时,点Q也同时以每秒2个单位长度的速度从点B向终点A运动,若PQ=![]() AB,求AP的长.
AB,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(操作发现)
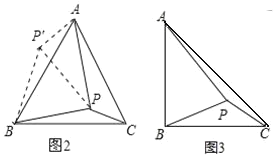
如图 1,在边长为 1 个单位长度的小正方形组成的网格中,ABC 的三个顶点均在格点上.现将ABC 绕点 A 按顺时针方向旋转 90°,点 B 的对应点为 B′,点 C 的对应点为 C′, 连接 BB′,如图所示则∠AB′B= .
(2)(解决问题)
如图 2,在等边ABC 内有一点 P,且 PA=2,PB=![]() ,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
(3)(灵活运用)
如图 3,将(2)题中“在等边ABC 内有一点 P 改为“在等腰直角三角形 ABC 内有一点P”,且 BA=BC,PA=6,BP=4,PC=2,求∠BPC 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
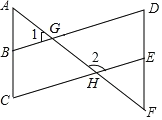
【题目】如图,已知AF分别与BD、CE交于点G、H,其中∠1+∠2=180°.
(1)判断BD和CE有怎样的位置关系,并说明理由;
(2)若∠A=∠F,探索∠C与∠D的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com