
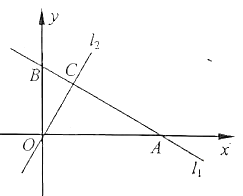
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象
的图象![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,正比例函数的图象
两点,正比例函数的图象![]() 与
与![]() 交于点
交于点![]() .
.
(1)求点![]() 坐标;
坐标;
(2)求![]() 的表达式;
的表达式;
(3)求![]() 和
和![]() 的面积.
的面积.
【答案】(1)C(2,4);(2) ![]() ;(3)
;(3) ![]() ;
;![]()
【解析】
(1)根据C点在![]() 上,将C点坐标代入
上,将C点坐标代入![]() 解析式,可得m的值,进而求出C点坐标;
解析式,可得m的值,进而求出C点坐标;
(2)由(1)得C点坐标,由待定系数法可以求出![]() 的解析式.
的解析式.
(3)过点C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,再根据A(10,0),B (0,5)可得AO=10,OB=5,进而求出![]() 和
和![]() 的面积.
的面积.
(1)把点C(m,4)代入一次函数![]() 中,得:
中,得:
![]()
解得:![]()
∴C(2,4)
(2)设![]() 的解析式为
的解析式为![]() ,将C(2,4)代入得:
,将C(2,4)代入得:
![]()
![]()
∴![]() 的解析式为:
的解析式为:![]() .
.
(3)如图,过点C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,
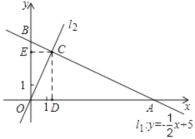
由![]() 得:
得:
![]() 时,
时,![]() ,即B (0,5);
,即B (0,5);
![]() 时,
时,![]() ,即A(10,0),
,即A(10,0),
∴AO=10,OB=5,
∴![]() ;
;
![]()


科目:初中数学 来源: 题型:
【题目】已知数轴上的A、B两点分别对应数字a、b,且a、b满足|4a-b|+(a-4)2=0
![]()
(1)a= ,b= ,并在数轴上面出A、B两点;
(2)若点P从点A出发,以每秒3个单位长度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B距离的2倍;
(3)数轴上还有一点C的坐标为30,若点P和点Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P点到达C点后,再立刻以同样的速度返回,运动到终点A.求点P和点Q运动多少秒时,P、Q两点之间的距离为4,并求此时点Q对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
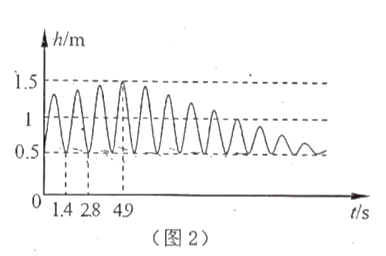
【题目】小明帮助小芳荡秋千(如图1),在小明的助推下,秋千越来越高,秋千离地面的高度![]() (
(![]() )与摆动时间
)与摆动时间![]() (
(![]() )之间的关系如图2所示.
)之间的关系如图2所示.
(1)根据函数定义,请判断变量![]() 是否为关于
是否为关于![]() 的函数?
的函数?
(2)结合图象回答:
①秋千静止时离地面的距离是多少?秋千的最高点与地面距离是多少?
②多长时间后小明就不再推小芳?
③从最低点开始向前和向后,再反悔到最低点,这叫做一个周期,请问,小芳完成第一个周期用了多长时间?
④每个周期的时间都是相等的,经过多长时间,秋千的最高点是1m?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、D是抛物线![]() 上两动点,点B、C在x轴上,且四边形ABCD是矩形,点E是抛物线与y轴的交点,连接BE交AD于点F,AD与y轴的交点为点G.设点A的横坐标为a(0<a<1).
上两动点,点B、C在x轴上,且四边形ABCD是矩形,点E是抛物线与y轴的交点,连接BE交AD于点F,AD与y轴的交点为点G.设点A的横坐标为a(0<a<1).
(1) 若矩形ABCD的周长为3.5,求a的值;
(2) 求证:不论点A如何运动,∠EAD=∠ABE;
(3) 若△ABE是等腰三角形,
①求点A的坐标;
②如图2,若将直线BA绕点B按逆时针方向旋转至直线l,设点A、C到直线l的距离分别为![]() 、
、![]() ,求
,求![]() 的最大值.
的最大值.
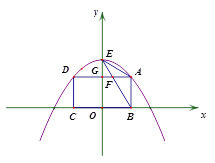
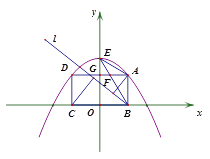
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着仰角为30°的山坡前进1000米到达D处,在D处测得山顶B的仰角为60°,求山的高度?
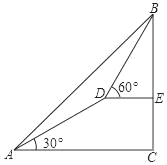
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=![]() AB.
AB.

探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接AB边上中线CE,由于CE=![]() AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.
(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣![]() ,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=
x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=![]() .
.
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)求S△OAB.
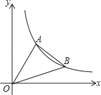
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张明暑假期间参加社会实践活动,从某批发市场以批发价每个m元的价格购进100个手机充电宝,然后每个加价n元到市场出售.
(1)求售出100个手机充电宝的总售价为多少元(结果用含m,n的式子表示)?
(2)由于开学临近,张明在成功售出60个充电宝后,决定将剩余充电宝按售价8折出售,并很快全部售完.
①她的总销售额是多少元?
②相比不采取降价销售,她将比实际销售多盈利多少元(结果用含m、n的式子表示)?
③若m=2n,张明实际销售完这批充电宝的利润率为 (利润率=利润÷进价×100%)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com