
����Ŀ����ͼ1����A��D��������![]() �������㣬��B��C��x���ϣ����ı���ABCD�Ǿ��Σ���E����������y��Ľ��㣬����BE��AD�ڵ�F��AD��y��Ľ���Ϊ��G�����A�ĺ�����Ϊa(0<a<1).
�������㣬��B��C��x���ϣ����ı���ABCD�Ǿ��Σ���E����������y��Ľ��㣬����BE��AD�ڵ�F��AD��y��Ľ���Ϊ��G�����A�ĺ�����Ϊa(0<a<1).
(1) ������ABCD���ܳ�Ϊ3.5����a��ֵ��
(2) ��֤�����۵�A����˶�����EAD����ABE��
(3) ����ABE�ǵ��������Σ�
�����A�����ꣻ
����ͼ2������ֱ��BA�Ƶ�B����ʱ�뷽����ת��ֱ��l�����A��C��ֱ��l�ľ���ֱ�Ϊ![]() ��
��![]() ����
����![]() �����ֵ.
�����ֵ.
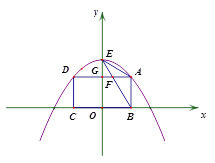
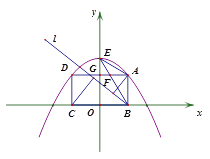
ͼ1 ͼ2
���𰸡�(1)a=0.5��(2) �������� (3)( ![]() ��
�� ![]() )
) ![]()
�������������������1��������y���������ߵĶԳ��ᣬҲ�Ǿ���ABCD�ĶԳ��ᣬ���ݾ��ε��ܳ��г����̼��ɽ�����⣻
��2����ͼ1�У����ȹ������κ���֤��![]() ��֤��
��֤��![]() �ĵ㹲Բ�����ɽ�����⣻
�ĵ㹲Բ�����ɽ�����⣻
��3���ٹ۲�ͼ�ο�֪��![]() �ǵ���������ʱ��ֻ��
�ǵ���������ʱ��ֻ��![]() ��
��![]() ������
�У�����![]() �ɵ�
�ɵ�![]() ���
���![]() ���ɽ�����⣮
���ɽ�����⣮
����ͼ3�У�����A��AM��ֱ��![]() ��
�� ![]() ֱ��
ֱ��![]() ��
��![]() ��
�� ![]() ֱ��
ֱ��![]() ��
��![]() ���ӳ�
���ӳ�![]() ��
��![]() ��
��![]() �����ı���
�����ı���![]() �Ǿ��Σ���
�Ǿ��Σ���![]() �Ƴ�
�Ƴ�![]() ����
����![]() �����ֵ��ֻҪ��
�����ֵ��ֻҪ��![]() �����ֵ���ɣ���
�����ֵ���ɣ���![]() ���
���![]() �غ�ʱ
�غ�ʱ![]() ��ֵ���.
��ֵ���.
�����������1��������![]() ���������ߵĶԳ��ᣬҲ�Ǿ���ABCD�ĶԳ��ᣬ
���������ߵĶԳ��ᣬҲ�Ǿ���ABCD�ĶԳ��ᣬ
��![]() ����
����![]() ��Գƣ�
��Գƣ�![]()
![]()
������![]()
���![]() ��
��![]() ����ȥ����
����ȥ����![]()
��2����ͼ1�У�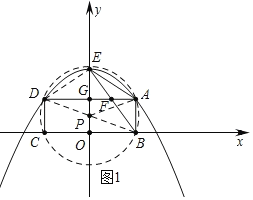
![]()
![]()
��ֱ��EB�Ľ���ʽΪ![]()
ֱ��DE�Ľ���ʽΪ![]()
![]()
![]() ��BD��OE��P��
��BD��OE��P��
��PG��AB�� ![]()
![]()
![]()
![]() �ĵ㹲Բ��
�ĵ㹲Բ��
![]()
![]() =
= ![]() ,
,![]()
��3���۲�ͼ�ο�֪��![]() �ǵ���������ʱ��ֻ��
�ǵ���������ʱ��ֻ��![]()
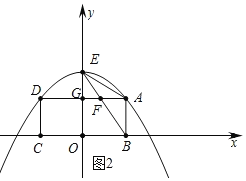
��![]() ��
�У� ![]()
![]()
���![]() ��
��![]() ����������
����������
���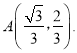
����ͼ3�У�����A��AM��ֱ��![]() ��
�� ![]() ֱ��
ֱ��![]() ��
��![]() ��
�� ![]() ֱ��
ֱ��![]() ��
��![]() ���ӳ�
���ӳ�![]() ��
��![]() ��
��![]() �����ı���
�����ı���![]() �Ǿ��Σ�
�Ǿ��Σ�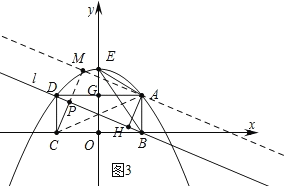
![]()
![]()
����![]()
![]() �����ֵ���ɣ�
�����ֵ���ɣ�
��![]() ��
�У� ![]()
�൱��![]() ���
���![]() �غ�ʱ
�غ�ʱ![]() ��ֵ���ʱ
��ֵ���ʱ![]()
![]() �����ֵ
�����ֵ


 53���ò�ϵ�д�
53���ò�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߹���ͼҪ��������ֱ����һ��������ֱ�ߵĴ��ߣ��������߶εĴ�ֱƽ���ߣ�
������ֱ����һ��������ֱ�ߵĴ��ߣ��������ǵ�ƽ���ߣ�
��ͼ�ǰ�����Ҫ������˳��ij߹���ͼ��

����ȷ������ǣ�������
A. �������������������������� B. ��������������������������
C. �������������������������� D. ��������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ������
������![]() ��
��![]() ��λ�ÿ�ʼ�Ƶ�
��λ�ÿ�ʼ�Ƶ�![]() ��˳ʱ�뷽����ת���ٶ���ÿ��
��˳ʱ�뷽����ת���ٶ���ÿ��![]() ��ͬʱ����
��ͬʱ����![]() ��
��![]() ��λ�ÿ�ʼ�Ƶ�
��λ�ÿ�ʼ�Ƶ�![]() ����ʱ�뷽����ת���ٶ���ÿ��
����ʱ�뷽����ת���ٶ���ÿ��![]() ������תʱ��Ϊ
������תʱ��Ϊ![]() ��
��![]() .
.
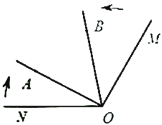
��1���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��
��![]() �Ķ�����
�Ķ�����
��2������ת�����У���![]() ����
����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��3������ת�������Ƿ����������![]() ��ʹ������
��ʹ������![]() ǡ����ͼ��ij���ǵ�ƽ���ߣ�������ڣ������
ǡ����ͼ��ij���ǵ�ƽ���ߣ�������ڣ������![]() ��ֵ����������ڣ���˵������.
��ֵ����������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ֱ֪��AB�ĺ�������ʽΪy=��2x+8����x�ύ�ڵ�A����y�ύ�ڵ�B��
��1����A��B��������ꣻ
��2������P��m��n��Ϊ�߶�AB�ϵ�һ�����㣨��A��B���غϣ�����PE��x���ڵ�E��PF��y���ڵ�F������EF���ʣ�
������PAO�����ΪS����S����m�ĺ�����ϵʽ����д��m��ȡֵ��Χ��
���Ƿ���ڵ�P��ʹEF��ֵ��С�������ڣ����EF����Сֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֵ��
��1����a=��1��b=2ʱ�������ʽ��2��ab��3b2����[6b2����ab��a2��]��ֵ
��2���Ȼ�������ֵ��4xy��2��![]() x2��3xy+2y2��+3��x2��2xy��������x��3��2+|y+1|=0����ʽ�ӵ�ֵ
x2��3xy+2y2��+3��x2��2xy��������x��3��2+|y+1|=0����ʽ�ӵ�ֵ
��3������2mx2��x+3������3x2��x��4���Ľ����x��ȡֵ�أ���m��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ȫ�����ѧ����������ѧУ��֯����С�飬��Ҫ���һѧ������μӣ���һѧ�깲���ĸ��࣬�μӵ�ѧ�����У�6a��3b���ˣ�����һ����a�˲μӣ�����μӵ�������һ��μӵ�����������b�ˣ�����μӵ������ȶ���μӵ�����һ���1�ˣ�
��1����������������ú�a��b��ʽ�ӱ�ʾ����
��2�����İ���������ú�a��b��ʽ�ӱ�ʾ����
��3�����ĸ��54�˲μ��˿��������������������ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
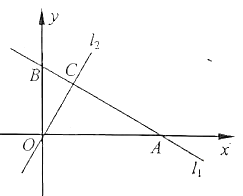
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���![]() ��ͼ��
��ͼ��![]() �ֱ���
�ֱ���![]() �ᡢ
�ᡢ![]() �ύ��
�ύ��![]() ���㣬������������ͼ��
���㣬������������ͼ��![]() ��
��![]() ���ڵ�
���ڵ�![]() .
.
��1�����![]() ���ꣻ
���ꣻ
��2����![]() �ı���ʽ��
�ı���ʽ��
��3����![]() ��
��![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪O��ֱ��AB��һ�㣬��BOC��90�㣬���ǰ壨MON����ֱ�Ƕ������ڵ�O���ֽ����ǰ����ŵ�O��ת��������OM��OC��ֱ��AB��ͬһ�࣮
��1������BOC��50��
����OMƽ�֡�BOCʱ�����AON�Ķ�����
����OM�ڡ�BOC�ڲ����ҡ�AON��3��COMʱ�����CON�Ķ�����
��2������COM��2��AONʱ���뻭��ʾ��ͼ�������AOM���BOC��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017���ϰ��긧���и���������Сѧ�����е�ְҵѧУ����չ������ʦ��������.ij�ؼҷ÷�ʽ�У�A.�����߷ã�B.�绰���ʣ�C.������ʣ��༶�Ż�QQȺ����D.����.���ؽ����ָ����˴�����ʦ�������ƽ̨�������ȡ����һ������ʦ�ļҷ��������������ͼ��ʾ�����в�������ͳ��ͼ.
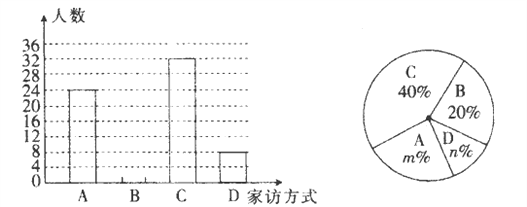
����ͼ���ṩ����Ϣ������������⣺
��1����α����ļҷ���ʦ���ж����ˣ�����ͳ��ͼ�У���A������Ӧ��Բ�ĽǵĶ���Ϊ���٣�
��2���벹ȫ����ͳ��ͼ.
��3����֪���ع���3500λ��ʦ�������������ʦ��������������Ƹ��ع��ж���λ��ʦ���õ��������߷õķ�ʽ���мҷõģ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com