
【题目】如图,在边长为3的等边△ABC中,点D在AC上,且CD=1,点E在AB上(不与点A、B重合),连接DE,把△ADE沿DE折叠,当点A的对应点F落在等边△ABC的边上时,AE的长为_____.
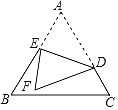
【答案】1或5﹣![]() .
.
【解析】
根据题意分类讨论,当F点落在边BC上时,证明△DFC∽△FEB,F点落在边AB上时,根据直角三角形的性质求解;
①当F点落在边BC上时,
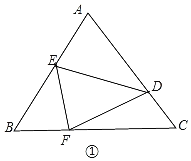
∵把△ADE沿DE折叠,
∴∠A=∠EFD=60°,
∵∠EFC=∠B+∠BEF,
∴∠EFD+∠DFC=∠B+∠BEF
∵∠EFD=∠A=∠B=60°,
∴∠DFC=∠BEF,
∴△DFC∽△FEB,
∴![]() ,
,
而EF+BE=EA+BE=AB=3,DF=DA=AC﹣CD=2,
∴![]() ,
,
解得AE=5﹣![]() ,或AE=5+
,或AE=5+![]() (舍去);
(舍去);
②F点落在边AB上时,
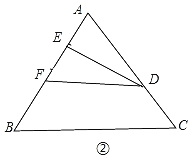
∵把△ADE沿DE折叠,
∴∠A=∠DFE=60°,∠DEA=90°,∠ADE=∠FDE,
∴∠ADE=30°,
∴AE=![]() AD=
AD=![]() (AC﹣CD)=
(AC﹣CD)=![]() ×2=1.
×2=1.
故A答案为1或5﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+3与y轴交于点A,与x轴交于点B,抛物线y=﹣
x+3与y轴交于点A,与x轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A和点B,过点A作AC⊥AB交抛物线于点C,过点C作CD⊥y轴于点D,点E在线段AC上,连接ED,且ED=EC,连接EB交y轴于点F.
x2+bx+c经过点A和点B,过点A作AC⊥AB交抛物线于点C,过点C作CD⊥y轴于点D,点E在线段AC上,连接ED,且ED=EC,连接EB交y轴于点F.
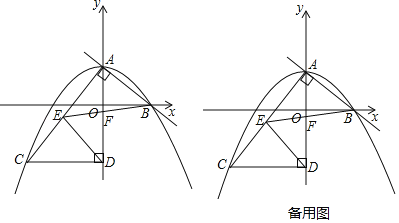
(1)求抛物线的表达式;
(2)求点C的坐标;
(3)若点G在直线AB上,连接FG,当∠AGF=∠AFB时,直接写出线段AG的长;
(4)在(3)的条件下,点H在线段ED上,点P在平面内,当△PAG≌△PDH时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,正方形ABCD的边长为6,点E,点F分别在边AB,AD上,AE=DF=2,连接DE,CF交于点G.连接AC与DE交于点M,延长CB至点K,使BK=3,连接GK交AB于点N.
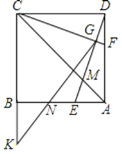
(1)求证:CF⊥DE;
(2)求△AMD的面积;
(3)请直接写出线段GN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P'是边AB上一点,四边形P'Q'M'N'是正方形,点Q',![]() 在边BC上,点N'在△ABC内.连接BN',并延长交AC于点N,NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.
在边BC上,点N'在△ABC内.连接BN',并延长交AC于点N,NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.
(1)求证:四边形PQMN为正方形;
(2)若∠A=90°,AC=1.5m,△ABC的面积=1.5m2.求PN的长.
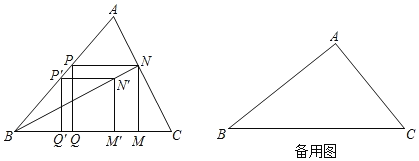
查看答案和解析>>
科目:初中数学 来源: 题型:
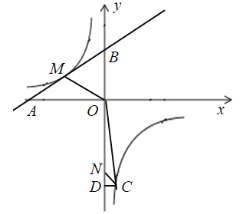
【题目】如图,一次函数![]() 的图像与
的图像与![]() 轴分别交于
轴分别交于![]() 两点,与反比例函数
两点,与反比例函数![]() 的图像交于点
的图像交于点![]() ,点C在反比例函数
,点C在反比例函数![]() 的图像上,过点C作
的图像上,过点C作![]() 轴于点D,连接
轴于点D,连接![]() ,已知
,已知![]() .
.
(1)![]() ,点A的坐标为________________.
,点A的坐标为________________.
(2)点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,且
,且![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2020年新冠肺炎疫情期间,我市某企业为支援湖北,准备将购买的70吨蔬菜运往武汉,现有甲、乙两种货车可以租用,已知2辆甲货车和3辆乙货车一次可运44吨蔬菜;3辆甲货车和1辆乙货车一次可运38吨蔬菜.
(1)求每辆甲种货车和每辆乙种货车一次分别能运多少吨蔬菜?
(2)已知甲种货车每辆租金500元,乙种货车每辆租金450元,该企业共租用甲、乙两种货车8辆,设租甲种货车a辆,求租车总费用w(元)与a之间的函数关系式,并求出自变量a的取值范围;
(3)在(2)的条件下,请你为该企业设计出费用最少的方案,并求出最少的租车费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,由顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第六个正方形A6B6C6D6周长是( )
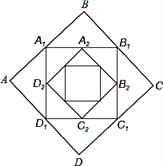
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)![]() ,
,![]() ;
;
(2)根据函数图象知,
①当![]() 时,
时,![]() 的取值范围是 ;
的取值范围是 ;
②当![]() 为 时,
为 时,![]() .
.
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 是反比例函数在第一象限的图象上一点,设直线
是反比例函数在第一象限的图象上一点,设直线![]() 与线段
与线段![]() 交于点
交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(4)点![]() 是
是![]() 轴上的一个动点,当△MBC为直角三角形时,直接写出点
轴上的一个动点,当△MBC为直角三角形时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂尔多斯市某百货商场销售某一热销商品A,其进货和销售情况如下:用16000元购进一批该热销商品A,上市后很快销售一空,根据市场需求情况,该商场又用7500元购进第二批该商品,已知第二批所购件数是第一批所购件数的一半,且每件商品的进价比第一批的进价少10元.
(1)求商场第二批商品A的进价;
(2)商场同时销售另一种热销商品B,已知商品B的进价与第二批商品A的进价相同,且最初销售价为165元,每天能卖出125件,经市场销售发现,若售价每上涨1元,其每天销售量就减少5件,问商场该如何定售价,每天才能获得最大利润?并求出每天的最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com