
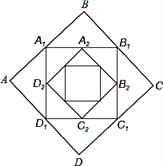
【题目】如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,由顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第六个正方形A6B6C6D6周长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据题意,利用中位线定理可证明顺次连接正方形ABCD四边中点得正方形![]() 的面积为正方形ABCD面积的一半,根据面积关系可得周长关系,以此类推可得正方形
的面积为正方形ABCD面积的一半,根据面积关系可得周长关系,以此类推可得正方形![]() 的周长.
的周长.
本题解析: 顺次连接正方形ABCD四边的中点得正方形![]() ,则得正方形
,则得正方形![]() 的面积为正方形ABCD面积的一半,即
的面积为正方形ABCD面积的一半,即![]() ,则周长是原来的
,则周长是原来的![]() ;
;
顺次连接正方形![]() 中点得正方形
中点得正方形![]() ,则正方形
,则正方形![]() 的面积为正方形
的面积为正方形![]() 面积的一半,即
面积的一半,即![]() ,则周长是原来的
,则周长是原来的![]() ;
;
顺次连接正方形![]() 得正方形
得正方形![]() ,则正方形
,则正方形![]() 的面积为正方形
的面积为正方形![]() 面积的一半,即
面积的一半,即![]() ,则周长是原来的
,则周长是原来的![]() ;
;
顺次连接正方形![]() 中点得正方形
中点得正方形![]() ,则正方形
,则正方形![]() 的面积为正方形
的面积为正方形![]() 面积的一半
面积的一半![]() ,则周长是原来的
,则周长是原来的![]() ;
;
…
故第n个正方形周长是原来的![]() ,
,
以此类推:第六个正方形![]() 周长是原来的
周长是原来的![]() ,
,
∵正方形ABCD的边长为1,
∴周长为4,
∴第六个正方形A6B6C6D6周长是![]() .
.
故答案为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 如图所示,点
如图所示,点![]() .
.
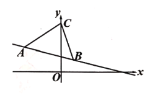
(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积;
的面积;
(3)一次函数![]() (
(![]() 为常数).
为常数).
①求证:一次函数![]() 的图象一定经过点
的图象一定经过点![]() ;
;
②若一次函数![]() 的图象与线段
的图象与线段![]() 有交点,直接写出
有交点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将每件进价为80元的某种商店按每件110元出售,每天可售出100件.该商店想通过降低售价、增加销售量的方法来提高利润.经市场调查,发现这种商品每件每降价5元,每天的销售量可增加50件.设商品降价x元,每天销售该商品获得的利润为y元.
(1)求y(元)关于x(元)的函数关系式,并写出x的取值范围.
(2)求当x取何值时y最大?并求出y的最大值.
(3)若要是每天销售利润为3750元,且尽可能最大的向顾客让利,应将该商品降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列五个命题:![]() 两个端点能够重合的弧是等弧;
两个端点能够重合的弧是等弧;![]() 圆的任意一条弧必定把圆分成劣弧和优弧两部分
圆的任意一条弧必定把圆分成劣弧和优弧两部分![]() 经过平面上任意三点可作一个圆;
经过平面上任意三点可作一个圆;![]() 任意一个圆有且只有一个内接三角形
任意一个圆有且只有一个内接三角形![]() 三角形的外心到各顶点距离相等.其中真命题有( )
三角形的外心到各顶点距离相等.其中真命题有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的动点(
边上的动点(![]() 不与
不与![]() 、
、![]() 重合),
重合),![]()

![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)![]() 与
与![]() 的大小关系为________.请证明你的结论;
的大小关系为________.请证明你的结论;
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长;
的长;
(4)是否存在![]() ,使
,使![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍?若存在,求出
倍?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和妈妈从家出发到长嘉汇观看国庆灯光秀,妈妈先出发,2分钟后小亮沿同一路线出发去追妈妈,当小亮追上妈妈时发现相机落在途中了,妈妈立即返回找相机,小亮继续前往长嘉汇,当小亮到达长嘉汇时,妈妈刚好找到了相机并立即前往长嘉汇(妈妈找相机的时间不计),小亮在长嘉汇等了一会,没有等到妈妈,就沿同一路线返回接妈妈,最终与妈妈会合,小亮和妈妈的速度始终不变,如图是小亮和妈妈两人之间的距离y(米)与妈妈出发的时间x(分钟)的图象;则小亮开始返回时,妈妈离家的距离为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润120元.为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱降价1元,每天可多售出2箱.
(1)如果要使每天销售饮料获利14000元,问每箱应降价多少元?
(2)每箱降价多少元超市每天获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
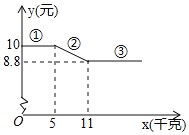
【题目】某水果店进行了一次水果促销活动,在该店一次性购买A种水果的单价y(元)与购买量x(千克)的函数关系如图所示,
(1)当0<x≤5时,单价y为 元.当单价y=8.8时,x的取值范围为 .
(2)根据函数图象,求第②段函数图象中单价y(元)与购买量(千克)的函数关系式,并写出x的取值范围.
(3)促销活动期间,张老师计划去该店购买A种水果10千克,那么张老师共需花费多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com