
【题目】在平面直角坐标系![]() 中,
中,![]() 如图所示,点
如图所示,点![]() .
.
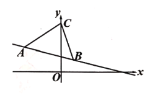
(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积;
的面积;
(3)一次函数![]() (
(![]() 为常数).
为常数).
①求证:一次函数![]() 的图象一定经过点
的图象一定经过点![]() ;
;
②若一次函数![]() 的图象与线段
的图象与线段![]() 有交点,直接写出
有交点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①见解析,②
;(3)①见解析,②![]() 且
且![]() .
.
【解析】
(1)根据待定系数求解析式即可;
(2)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 点,求出点D的坐标,然后根据
点,求出点D的坐标,然后根据![]() 可得出结果;
可得出结果;
(3)①把一次函数![]() 整理为
整理为![]() 的形式,再令x+3=0,求出y的值即可;
的形式,再令x+3=0,求出y的值即可;
②根据直线![]() 一定经过点A,而且与线段BC有交点,可得直线
一定经过点A,而且与线段BC有交点,可得直线![]() 在绕着点A从直线AC顺时针旋转到直线BC之间的区域,再结合a≠0从而得出结果.
在绕着点A从直线AC顺时针旋转到直线BC之间的区域,再结合a≠0从而得出结果.
解:(1)设直线![]() 的解析式是
的解析式是![]() ,将点
,将点![]() ,点
,点![]() 代入的,得
代入的,得
![]() ,解得,
,解得,
∴直线![]() 的解析式是
的解析式是![]() ;
;
(2)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 点,
点,
则点![]() 的坐标为
的坐标为![]() ,
,
![]() ;
;
(3)①证明:∵![]() ,
,
令x+3=0,得x=-3,此时y=2.
∴![]() 必过点
必过点![]() ,即必过
,即必过![]() 点;
点;
②当直线![]() 与直线AC重合时,可得4=3a+2,解得a=
与直线AC重合时,可得4=3a+2,解得a=![]() ,
,
当直线![]() 与直线AB重合时,可得1=a+3a+2,解得a=
与直线AB重合时,可得1=a+3a+2,解得a=![]() ,
,
∴a的取值范围是:![]() 且
且![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.
(1)每台A,B两种型号的机器每小时分别加工多少个零件?
(2)如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E为AB的中点,F为线段BE上任意一点,将线段EF绕点E逆时针旋转90°,得到线段EG.

(1)按请按要求补全图形:连接BG过点G作GH⊥BG,交对角线AC于点H,连接DH;
(2)判断DH与GH的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为_____m2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组条件中,能够判定△ABC≌△DEF 的是( )
A. ∠A=∠D,∠B=∠E,∠C=∠FB. AB=DE,BC=EF,∠A=∠D
C. ∠B=∠E=90°,BC=EF,AC=DFD. ∠A=∠D,AB=DF,∠B=∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
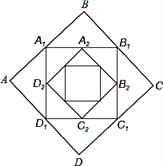
【题目】如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,由顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第六个正方形A6B6C6D6周长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知平面内一点![]() 与一直线
与一直线![]() ,如果过点
,如果过点![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,那么垂足
,那么垂足![]() 叫做点
叫做点![]() 在直线
在直线![]() 上的射影;如果线段
上的射影;如果线段![]() 的两个端点
的两个端点![]() 和
和![]() 在直线
在直线![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么线段
,那么线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的射影.
上的射影.
如图①,已知平面内一点![]() 与一直线
与一直线![]() ,如果过点
,如果过点![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,那么垂足
,那么垂足![]() 叫做点
叫做点![]() 在直线
在直线![]() 上的射影;如果线段
上的射影;如果线段![]() 的两个端点
的两个端点![]() 和
和![]() 在直线
在直线![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么线段
,那么线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的射影.
上的射影.
![]() 如图②,
如图②,![]() 、
、![]() 为线段
为线段![]() 外两点,
外两点,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.
则![]() 点在
点在![]() 上的射影是________点,
上的射影是________点,![]() 点在
点在![]() 上的射影是________点,
上的射影是________点,
线段![]() 在
在![]() 上的射影是________,线段
上的射影是________,线段![]() 在
在![]() 上的射影是________;
上的射影是________;
![]() 根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
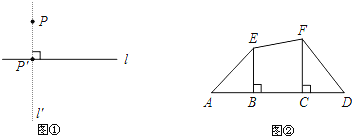
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com