【题目】在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=xm．若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），则花园面积S的最大值为_____m2．
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案科目：初中数学 来源： 题型：
【题目】如图所示，直线
交
轴于点
，在
轴正方向上取点
，使
；过点作
轴，交
于点
，在轴正方向上取点
，使
；过点作
轴，交于点
，…记
面积为
，
面积为
，
面积为
，…，则
等于（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
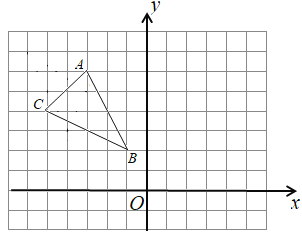
【题目】在如图所示的正方形网格中，每个小正方形的边长都是1，已知三角形
的三个顶点的坐标分别为
，
，
（1）作出三角形关于
轴对称的三角形
（2）点
的坐标为 .
（3）①利用网络画出线段
的垂直平分线
；②
为直线上上一动点，则
的最小值为 .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y＝
x+3的图象分别与y轴，x轴交于点A，B，点P从点B出发，沿射线BA以每秒1个单位的速度运动，设点P的运动时间为t秒．
（1）点P在运动过程中，若某一时刻，△OPA的面积为3，求此时P的坐标；
（2）在整个运动过程中，当t为何值时，△AOP为等腰三角形？请直接写出t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，
如图所示，点
.
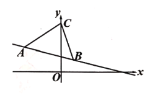
（1）求直线
的解析式；
（2）求的面积；
（3）一次函数
（
为常数）.
①求证：一次函数的图象一定经过点
；
②若一次函数的图象与线段
有交点，直接写出的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线y＝﹣
x+3与x轴、y轴分别交于A、C，以OA、OC为边在第一象限内作长方形OABC．
（1）将△ABC沿B′D对折，使得点A与点C重合，折痕交AB于点D，求直线CD的解析式；
（2）若在x轴上存在点P，使△ADP为等腰三角形，求出符合条件的点P坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店将每件进价为80元的某种商店按每件110元出售，每天可售出100件．该商店想通过降低售价、增加销售量的方法来提高利润．经市场调查，发现这种商品每件每降价5元，每天的销售量可增加50件．设商品降价x元，每天销售该商品获得的利润为y元．
（1）求y（元）关于x（元）的函数关系式，并写出x的取值范围．
（2）求当x取何值时y最大？并求出y的最大值．
（3）若要是每天销售利润为3750元，且尽可能最大的向顾客让利，应将该商品降价多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
中，
，
，点
为
边上的动点（不与
、
重合），
，
交
于点
．
（1）
与
的大小关系为________．请证明你的结论；
（2）设
，
，求
关于
的函数关系式，并写出自变量的取值范围；
（3）当
是等腰三角形时，求
的长；
（4）是否存在，使
的面积是
面积的
倍？若存在，求出的值，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ABC=
,BC=6cm，AC=10cm。
（1）求AB的长；
（2）若P点从点B出发，以2cm/s的速度在BC所在的直线
上运动，设运动时间为t秒，那么当t为何值时，△ACP为等腰三角形。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
