
【题目】如图,已知直线y=﹣![]() x+3与x轴、y轴分别交于A、C,以OA、OC为边在第一象限内作长方形OABC.
x+3与x轴、y轴分别交于A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)将△ABC沿B′D对折,使得点A与点C重合,折痕交AB于点D,求直线CD的解析式;
(2)若在x轴上存在点P,使△ADP为等腰三角形,求出符合条件的点P坐标.
【答案】(1)y=﹣![]() x+3;(2)P点的坐标是(﹣
x+3;(2)P点的坐标是(﹣![]() ,0)或(
,0)或(![]() ,0)
,0)
【解析】
(1)已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,即可求得A和C的坐标;根据题意可知△ACD是等腰三角形,算出AD长即可求得D点坐标,最后即可求出CD的解析式;
(2)由于△ADP是等腰直角三角形且∠DAP=90°,所以只要AD=AP.
(1)令y=0,则![]() x+3=0,解得:x=2,
x+3=0,解得:x=2,
∴A(2,0),
令x=0,则y=3,
∴C(0,3);
由折叠可知:CD=AD,
设AD=x,则CD=x,BD=3﹣x,
由题意得:(3﹣x)2+22=x2,
解得:x![]() ,
,
此时AD![]() ,
,
∴D(2,![]() ),
),
设直线CD为y=kx+3,
把D(2,![]() )代入得:
)代入得:![]() 2k+3,
2k+3,
解得:k![]() ,
,
∴直线CD的解析式为y![]() x+3;
x+3;
(2)∵A(2,0),D(2,![]() ),
),
∴AD![]() .
.
∵∠DAP=90°,
∴△ADP是等腰直角三角形,
∴AD=AP![]() ,
,
∴P点的坐标是(![]() ,0)或(
,0)或(![]() ,0).
,0).



科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点(A在B的左侧),其中点B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)将抛物线向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线上且在x轴上方的任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲将![]() 件产品全部运往甲,乙,丙三地销售(每地均有产品销售),运费分别为40元/件,24元/件,7元/件,且要求运往乙地的件数是运往甲地件数的3倍,设安排
件产品全部运往甲,乙,丙三地销售(每地均有产品销售),运费分别为40元/件,24元/件,7元/件,且要求运往乙地的件数是运往甲地件数的3倍,设安排![]() (
(![]() 为正整数)件产品运往甲地.
为正整数)件产品运往甲地.
(1)根据信息填表:
甲地 | 乙地 | 丙地 | |
产品件数(件) |
|
| |
运费(元) |
|
(2)若总运费为6300元,求![]() 与
与![]() 的函数关系式并求出
的函数关系式并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为_____m2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点在格点上.
(1)作出与△ABC关于x轴对称的图形△A1B1C1;
(2)求出A1,B1,C1三点坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
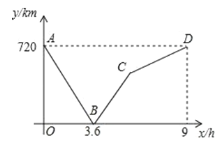
【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.两车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,图中的折线表示
,图中的折线表示![]() 与
与![]() 之间的函数关系,根据图象解决以下问题:
之间的函数关系,根据图象解决以下问题:
(1)甲、乙两地的距离为 ![]() .
.
(2)慢车的速度为 ![]() ,快车的速度为
,快车的速度为 ![]() ;
;
(3)求当![]() 为多少时,两车之间的距离为
为多少时,两车之间的距离为![]() ,请通过计算求出
,请通过计算求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com