练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

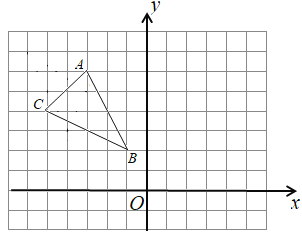
    【题目】在如图所示的正方形网格中，每个小正方形的边长都是1，已知三角形的三个顶点的坐标分别为，，

    （1）作出三角形关于轴对称的三角形

    （2）点的坐标为 .

    （3）①利用网络画出线段的垂直平分线；②为直线上上一动点，则的最小值为 .

    【答案】（1）见解析（2）点的坐标为；（3）①见解析②.

    【解析】

    （1）首先确定A、B、C三点关于y轴的对称点位置A1、B1、C1，再连接即可得到△ABC关于y轴对称的△A1B1C1；

    （2）根据平面直角坐标系写出点的坐标；

    （3）①根据垂直平分线的定义画图即可；

    ②根据轴对称的性质以及两点之间线段最短得的最小值为BC的长，再由勾股定理求解即可.

    （1）如图所示：

    （2）点的坐标为；

    （3）①如图所示：

    ②的最小值为BC的长，即BC=.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

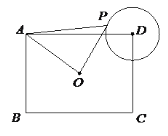
    【题目】如图，在矩形ABCD中，AB=3，BC=4，O为矩形ABCD的中心，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP，则△AOP面积的最大值为（　　）

    A. 4 B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

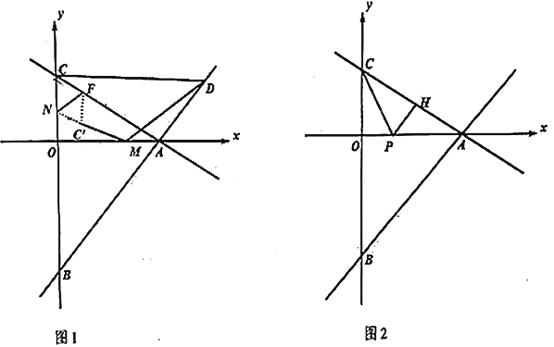
    【题目】如图1，已知直线和直线交于轴上一点，且分别交轴于点、点，且.

    （1）求的值；

    （2）如图1，点是直线上一点，且在轴上方，当时，在线段上取一点，使得，点分别为轴、轴上的动点，连接，将沿翻折至，求的最小值；

    （3）如图2，分别为射线上的动点，连接是否存在这样的点，使得为等腰三角形，为直角三角形同时成立.请直接写出满足条件的点坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在一个可以自由转动的转盘中，指针位置固定，三个扇形的面积都相等，且分别标有数字1，2，3．

    （1）小明转动转盘一次，当转盘停止转动时，指针所指扇形中的数字是奇数的概率为________；

    （2）小明先转动转盘一次，当转盘停止转动时，记录下指针所指扇形中的数字；接着再转动转盘一次，当转盘停止转动时，再次记录下指针所指扇形中的数字，求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）|﹣2|+tan30°+（2018﹣π）0-（）-1

    （2）先化简，再求值：（﹣1）÷，其中x的值从不等式组的整数解中选取．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣x2+bx+c与x轴交于A，B两点（A在B的左侧），其中点B（3，0），与y轴交于点C（0，3）．

    （1）求抛物线的解析式；

    （2）将抛物线向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），求h的取值范围；

    （3）设点P是抛物线上且在x轴上方的任一点，点Q在直线l：x=﹣3上，△PBQ能否成为以点P为直角顶点的等腰直角三角形？若能，求出符合条件的点P的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰的顶角的度数是，点是腰的黄金分割点，将绕着点按照顺时针方向旋转一个角度后点落在点处，联结，当时，这个旋转角是________度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=xm．若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），则花园面积S的最大值为_____m2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E是正方形ABCD中CD边上一点，以点A为中心把△ADE顺时针旋转90°。

    （1）在图中画出旋转后的图形；

    （2）若旋转后E点的对应点记为M，点F在BC上，且∠EAF=45°，连接EF。

    ①求证：△AMF≌△AEF；

    ②若正方形的边长为6，AE＝，求EF的长．

    查看答案和解析>>

    同步练习册答案