
【题目】已知:如图,在同心圆中,大圆的弦AB交小圆于C、D两点.
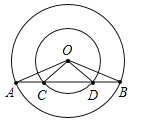
(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.
【答案】(1)证明见试题解析;(2)AC=BD,证明见试题解析.
【解析】
(1)由于OA=OB,OC=OD,利用等边对等角易得∠A=∠B,∠OCD=∠ODC,而利用三角形外角性质可得∠OCD=∠A+∠AOC,∠ODC=∠BOD+∠B,从而可得∠A+∠AOC=∠BOD+∠B,再利用等量相减,差相等可得∠AOC=∠DOB;
(2)过O作OE⊥AB于E,利用垂径定理有AE=EB,CE=ED,于是AE-CE=BE-DE,即AC=BD.
试题解析:
(1)∵AO=OB,OC=OD
∴∠A=∠B,∠OCD=∠ODC
∴∠OCA=∠ODC
∴△ACO≌△ODB
∴∠AOC=∠DOB
(2)过O作OE⊥AB于E
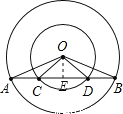
∴AE=EB,CE=ED
∴AC=BD


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
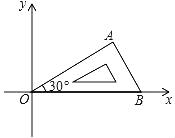
【题目】将含有 30°角的直角三角板 OAB 如图放置在平面直角坐标系中,OB 在 x轴上,若 OA=2,将三角板绕原点 O 顺时针旋转 75°,则点 A 的对应点 A′ 的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(–1,3),与x轴的交点A在点(–3,0)和(–2,0)之间,以下结论:①b2–4ac=0;②a+b+c>0;③2a–b=0;④c–a=3.其中正确的有( )
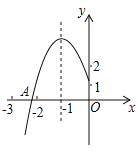
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
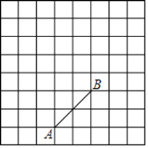
(1)将线段AB向上平移两个单位长度,点A的对应点为点A1,点B的对应点为点B1,请画出平移后的线段A1B1;
(2)将线段A1B1绕点A1按逆时针方向旋转90°,点B1的对应点为点B2,请画出旋转后的线段A1B2;
(3)连接AB2、BB2,求△ABB2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区有一块长方形水稻试验田,试验田的长、宽(如图所示,长度单位:米),试验田分两部分,一部分为水渠,另一部分为新型水稻种植田(阴影部分).
(1)用含a,b的式子表示新型水稻种植田的面积是多少平方米(结果化成最简形式);
(2)若a=30,b=40,在“农民丰收节”到来之时水稻成熟,计划先由甲型收割机收割一部分,再由乙型收割机收割剩余部分,甲型收割机收割水稻每平方米的费用为0.3元,乙型收割机收割水稻每平方米的费用为0.5元,若要收割全部水稻的费用不超过5000元,问甲型收割机最少收割多少平方米的水稻?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件求二次函数解析式
(1)已知一个二次函数的图象经过了点A(0,﹣1),B(1,0),C(﹣1,2);
(2)已知抛物线顶点P(﹣1,﹣8),且过点A(0,﹣6);
查看答案和解析>>
科目:初中数学 来源: 题型:
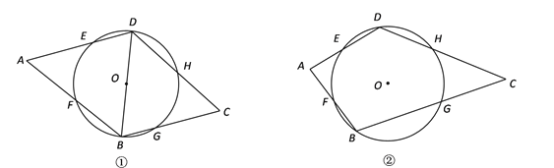
【题目】已知⊙O经过四边形ABCD的B、D两点,并与四条边分别交于点E、F、G、H,且![]() .
.
(1)如图①,连接BD,若BD是⊙O的直径,求证:∠A=∠C;
(2)如图②,若![]() 的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com