
ЁОЬтФПЁПФГЕиЧјгавЛПщГЄЗНаЮЫЎЕОЪдбщЬяЃЌЪдбщЬяЕФГЄЁЂПэЃЈШчЭМЫљЪОЃЌГЄЖШЕЅЮЛЃКУзЃЉЃЌЪдбщЬяЗжСНВПЗжЃЌвЛВПЗжЮЊЫЎЧўЃЌСэвЛВПЗжЮЊаТаЭЫЎЕОжжжВЬяЃЈвѕгАВПЗжЃЉЃЎ
ЃЈ1ЃЉгУКЌaЃЌbЕФЪНзгБэЪОаТаЭЫЎЕОжжжВЬяЕФУцЛ§ЪЧЖрЩйЦНЗНУзЃЈНсЙћЛЏГЩзюМђаЮЪНЃЉЃЛ
ЃЈ2ЃЉШєaЃН30ЃЌbЃН40ЃЌдкЁАХЉУёЗсЪеНкЁБЕНРДжЎЪБЫЎЕОГЩЪьЃЌМЦЛЎЯШгЩМзаЭЪеИюЛњЪеИювЛВПЗжЃЌдйгЩвваЭЪеИюЛњЪеИюЪЃгрВПЗжЃЌМзаЭЪеИюЛњЪеИюЫЎЕОУПЦНЗНУзЕФЗбгУЮЊ0.3дЊЃЌвваЭЪеИюЛњЪеИюЫЎЕОУПЦНЗНУзЕФЗбгУЮЊ0.5дЊЃЌШєвЊЪеИюШЋВПЫЎЕОЕФЗбгУВЛГЌЙ§5000дЊЃЌЮЪМзаЭЪеИюЛњзюЩйЪеИюЖрЩйЦНЗНУзЕФЫЎЕОЃП

ЁОД№АИЁПЃЈ1ЃЉ11b2Љ5abЃЛЃЈ2ЃЉМзаЭЪеИюЛњзюЩйЪеИю4000ЦНЗНУзЕФЫЎЕОЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгУДѓОиаЮЕФУцЛ§МѕШЅаЁОиаЮЕФУцЛ§СаГіЫуЪНЃЌдйЛЏМђМДПЩЕУЃЛ
ЃЈ2ЃЉЯШНЋaЃЌbЕФжЕДњШыЃЈ1ЃЉжаЛЏМђЕФДњЪ§ЪНЧѓГіЫЎЕОЕФУцЛ§ЃЌдйЩшМзаЭЪеИюЛњЪеИюЫЎЕОaЦНЗНУзЃЌдђвваЭЪеИюЛњЪеИюЫЎЕОУцЛ§ЮЊЃЈ11600-aЃЉЦНЗНУзЃЌИљОнЪеИюШЋВПЫЎЕОЕФЗбгУВЛГЌЙ§5000дЊСаГіВЛЕШЪНЃЌНтжЎПЩЕУЃЎ
ЃЈ1ЃЉаТаЭЫЎЕОжжжВЬяЕФУцЛ§ЮЊЃЈ3b+bЉaЃЉЃЈ2b+bЉaЃЉЉЃЈbЉaЃЉ2
ЃНЃЈ4bЉaЃЉЃЈ3bЉaЃЉЉЃЈbЉaЃЉ2
ЃН12b2Љ4abЉ3ab+a2Љb2+2abЉa2
ЃН11b2Љ5abЃЛ
ЃЈ2ЃЉЕБaЃН30ЃЌbЃН40ЪБЃЌаТаЭЫЎЕОжжжВЬяЕФУцЛ§11b2Љ5abЃН11600ЃЈЦНЗНУзЃЉЃЌ
ЩшМзаЭЪеИюЛњЪеИюЫЎЕОaЦНЗНУзЃЌдђвваЭЪеИюЛњЪеИюЫЎЕОУцЛ§ЮЊЃЈ11600ЉaЃЉЦНЗНУзЃЌ
ИљОнЬтвтЃЌЕУЃК0.3a+0.5ЃЈ11600ЉaЃЉЁм5000ЃЌ
НтЕУЃКaЁн4000ЃЌ
Д№ЃКМзаЭЪеИюЛњзюЩйЪеИю4000ЦНЗНУзЕФЫЎЕОЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЛЭЈЙЄГЬбЇРэТлАбдкЕЅЯђЕРТЗЩЯааЪЛЕФЦћГЕПДГЩСЌајЕФвКЬхЃЌВЂгУСїСПЁЂЫйЖШЁЂУмЖШШ§ИіИХФюУшЪіГЕСїЕФЛљБОЬиеїЁЃЦфжаСїСПqЃЈСО/аЁЪБЃЉжИЕЅЮЛЪБМфФкЭЈЙ§ЕРТЗжИЖЈЖЯУцЕФГЕСОЪ§ЃЛЫйЖШvЃЈЧЇУз/аЁЪБЃЉжИЭЈЙ§ЕРТЗжИЖЈЖЯУцЕФГЕСОЫйЖШЃЛУмЖШЃЈСО/ЧЇУзЃЉжИЭЈЙ§ЕРТЗжИЖЈЖЯУцЕЅЮЛГЄЖШФкЕФГЕСОЪ§ЃЌЮЊХфКЯДѓЪ§ОнжЮЖТааЖЏЃЌВтЕУФГТЗЖЮСїСПqгыЫйЖШvжЎМфЕФВПЗжЪ§ОнШчЯТБэЃК
ЫйЖШvЃЈЧЇУз/аЁЪБЃЉ | Ё | 5 | 10 | 20 | 32 | 40 | 48 | Ё |
СїСПqЃЈСО/аЁЪБЃЉ | Ё | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | Ё |
ЃЈ1ЃЉИљОнЩЯБэаХЯЂЃЌЯТСаШ§ИіКЏЪ§ЙиЯЕЪНжаЃЌПЬЛqЃЌvЙиЯЕзюзМШЗЕФЪЧЃЈжЛашЬюЩЯе§ШЗД№АИЕФађКХЃЉЂй ![]() Ђк
Ђк ![]() Ђл
Ђл ![]()
ЃЈ2ЃЉЧыРћгУЃЈ1ЃЉжабЁШЁЕФКЏЪ§ЙиЯЕЪНЗжЮіЃЌЕБИУТЗЖЮЕФГЕСїЫйЮЊЖрЩйЪБЃЌСїСПДяЕНзюДѓЃПзюДѓСїСПЪЧЖрЩйЃП
ЃЈ3ЃЉвбжЊqЃЌvЃЌkТњзу ![]() ЃЌЧыНсКЯЃЈ1ЃЉжабЁШЁЕФКЏЪ§ЙиЯЕЪНМЬајНтОіЯТСаЮЪЬтЃК
ЃЌЧыНсКЯЃЈ1ЃЉжабЁШЁЕФКЏЪ§ЙиЯЕЪНМЬајНтОіЯТСаЮЪЬтЃК
ЂйЪаНЛЭЈдЫааМрПиЦНЬЈЯдЪОЃЌЕБ ![]() ЪБЕРТЗГіЯжЧсЖШгЕЖТЃЌЪдЗжЮіЕБГЕСїУмЖШkдкЪВУДЗЖЮЇЪБЃЌИУТЗЖЮГіЯжЧсЖШгЕЖТЃЛ
ЪБЕРТЗГіЯжЧсЖШгЕЖТЃЌЪдЗжЮіЕБГЕСїУмЖШkдкЪВУДЗЖЮЇЪБЃЌИУТЗЖЮГіЯжЧсЖШгЕЖТЃЛ
ЂкдкРэЯызДЬЌЯТЃЌМйЩшЧАКѓСНГЕГЕЭЗжЎМфЕФОрРыdЃЈУзЃЉОљЯрЕШЃЌЧѓСїСПqзюДѓЪБdЕФжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊAЁЂBСНЕуЕФзјБъЗжБ№ЮЊЃЈ2ЃЌ0ЃЉЁЂЃЈ0ЃЌ4ЃЉЃЌPЪЧЁїAOBЭтНгдВЁбCЩЯЕФвЛЕуЃЌЧвЁЯAOP=45ЁуЃЌдђЕуPЕФзјБъЮЊ ЃЎ 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпAMЁЭANЃЌABЦНЗжЁЯMANЃЌЙ§ЕуBзїBCЁЭBAНЛANгкЕуCЃЛЖЏЕуEЁЂDЭЌЪБДгAЕуГіЗЂЃЌЦфжаЖЏЕуEвд2cm/sЕФЫйЖШбиЩфЯпANЗНЯђдЫЖЏЃЌЖЏЕуDвд1cm/sЕФЫйЖШдкжБЯпAMЩЯдЫЖЏЃЛвбжЊAC=6cmЃЌЩшЖЏЕуDЃЌEЕФдЫЖЏЪБМфЮЊtsЃЎ
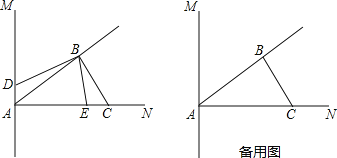
ЃЈ1ЃЉЪдЧѓЁЯACBЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШє![]() ЃК
ЃК![]() =2ЃК3ЃЌЪдЧѓЖЏЕуDЃЌEЕФдЫЖЏЪБМфtЕФжЕЃЛ
=2ЃК3ЃЌЪдЧѓЖЏЕуDЃЌEЕФдЫЖЏЪБМфtЕФжЕЃЛ
ЃЈ3ЃЉЪдЮЪЕБЖЏЕуDЃЌEдкдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГИіЪБМфtЃЌЪЙЕУЁїADBЁеЁїCEBЃПШєДцдкЃЌЧыЧѓГіЪБМфtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕГіРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌвбжЊЁїOABЪЧЕШбќжБНЧШ§НЧаЮЃЌЧвЁЯOABЃН90ЁуЃЌШєЕуAЕФзјБъЃЈ3ЃЌ1ЃЉЃЌдђЕуBЕФзјБъЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ1ЃЌЗжБ№вдЖЅЕуAЁЂBЁЂCЁЂDЮЊдВаФЃЌ1ЮЊАыОЖЛЛЁЃЌЫФЬѕЛЁНЛгкЕуEЁЂFЁЂGЁЂHЃЌдђЭМжавѕгАВПЗжЕФЭтЮЇжмГЄЮЊЃЈЁЁЁЁЃЉ
A.![]()
B.![]()
C.Іа
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁЯ1+ЁЯ2=180ЁуЃЌЁЯDAE=ЁЯBCFЃЌDAЦНЗжЁЯBDFЃЎ
ЃЈ1ЃЉAEгыFCЛсЦНааТ№?ЫЕУїРэгЩЃЎ
ЃЈ2ЃЉADгыBCЕФЮЛжУЙиЯЕШчКЮ?ЮЊЪВУД?
ЃЈ3ЃЉBCЦНЗжЁЯDBEТ№?ЮЊЪВУДЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаBDЁЂCDЦНЗжЁЯABCЁЂЁЯACBЃЌЙ§DзїжБЯпЦНаагкBCЃЌНЛABЁЂACгкEЁЂFЃЌЕБЁЯAЕФЮЛжУМАДѓаЁБфЛЏЪБЃЌЯпЖЮEFКЭBE+CFЕФДѓаЁЙиЯЕЃЈЁЁЁЁЃЉ
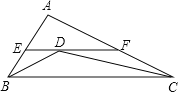
A. ![]() B.
B. ![]() C.
C. ![]() D. ВЛФмШЗЖЈ
D. ВЛФмШЗЖЈ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЕуDдкЁїABCЕФФкВПЧвDB=DCЃЌЕуEЃЌFдкЁїABCЕФЭтВПЃЌFB=FAЃЌEA=ECЃЌЁЯFBA=ЁЯDBC=ЁЯECAЃЎ
ЃЈ1ЃЉЂйЬюПеЃКЁїACEЁзЁзЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїCDEЁзЁїCBAЃЛ
ЃЈ3ЃЉЧѓжЄЃКЁїFBDЁеЁїEDCЃЛ
ЃЈ4ЃЉШєЕуDдкЁЯBACЕФЦНЗжЯпЩЯЃЌХаЖЯЫФБпаЮAFDEЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com