
【题目】如图,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度在直线AM上运动;已知AC=6cm,设动点D,E的运动时间为ts.
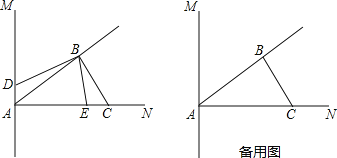
(1)试求∠ACB的度数;
(2)若![]() :
:![]() =2:3,试求动点D,E的运动时间t的值;
=2:3,试求动点D,E的运动时间t的值;
(3)试问当动点D,E在运动过程中,是否存在某个时间t,使得△ADB≌△CEB?若存在,请求出时间t的值;若不存在,请说出理由.
【答案】(1)45°.(2)当t=![]() s时,满足S△ADB:S△BEC=2:3.(3)存在.当t=2s 或t=6s时,△ADB≌△CEB.
s时,满足S△ADB:S△BEC=2:3.(3)存在.当t=2s 或t=6s时,△ADB≌△CEB.
【解析】
(1)易求∠BAC=45°,根据BC⊥BA可得∠ABC=90°,即可解题;
(2)作BF⊥AM,BG⊥AC,则BF=BG,根据S△ABD:S△BEC的值可得AD:CE的值,分别用t表示AD,CE即可求得t的值,即可解题;
(3)易得AD=CE时,△ADB≌△BEC,分别用t表示AD,CE即可求得t的值,即可解题.
解:(1)如图1中,
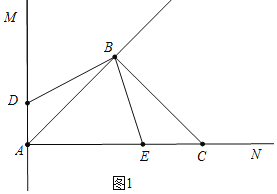
∵AM⊥AN,
∴∠MAN=90°,
∵AB平分∠MAN,
∴∠BAC=45°,
∵CB⊥AB,
∴∠ABC=90°,
∴∠ACB=45°.
(2)如图2中,
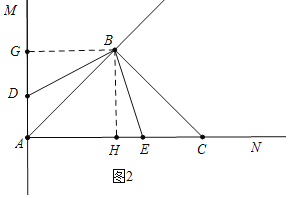
作BH⊥AC于H,BG⊥AM于G.
∵BA平分∠MAN,
∴BG=BH,
∵S△ADB:S△BEC=2:3,AD=t,AE=2t,
∴![]() tBG:
tBG:![]() (6-2t)BH=2:3,
(6-2t)BH=2:3,
∴t=![]() s.
s.
∴当t=![]() s时,满足S△ADB:S△BEC=2:3.
s时,满足S△ADB:S△BEC=2:3.
(3)存在.理由如下
①当点D在点A上方,且点E在点C左侧时,AD=t,EC=6-2t,
∵BA=BC,∠BAD=∠BCE=45°,
∴当AD=EC时,△ADB≌△CEB,
∴t=6-2t,
∴t=2s,
∴t=2s时,△ADB≌△CEB.
②当点D在点A下方,且点E在点C右侧时,AD=t,EC=2t-6,
∵BA=BC,∠BAD=∠BCE=135°,
∴当AD=EC时,△ADB≌△CEB,
∴t=2t-6,
∴t=6s,
∴t=6s时,△ADB≌△CEB.
∴综上所述:当t=2s 或t=6s时,△ADB≌△CEB.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,CE,BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3……
第n次操作,分别作∠ABEn-1和∠DCEn-1的平分线,交点为En.

(1)如图①,求证:∠E=∠B+∠C;
(2)如图②,求证:∠E1=![]() ∠E;
∠E;
(3)猜想:若∠En=b°,求∠BEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
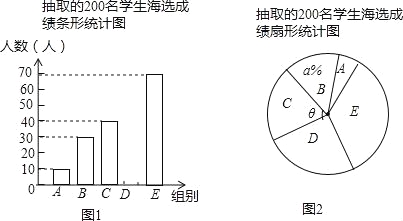
【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
组别 | 海选成绩x |
A组 | 50≤x<60 |
B组 | 60≤x<70 |
C组 | 70≤x<80 |
D组 | 80≤x<90 |
E组 | 90≤x<100 |
请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角θ的度数为 度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.

(1)求该一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为⊙O的直径,弦AB垂直于CD,垂足为H,∠EAD=∠HAD. 
(1)求证:AE为⊙O的切线;
(2)延长AE与CD的延长线交于点P,过D 作DE⊥AP,垂足为E,已知PA=2,PD=1,求⊙O的半径和DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区有一块长方形水稻试验田,试验田的长、宽(如图所示,长度单位:米),试验田分两部分,一部分为水渠,另一部分为新型水稻种植田(阴影部分).
(1)用含a,b的式子表示新型水稻种植田的面积是多少平方米(结果化成最简形式);
(2)若a=30,b=40,在“农民丰收节”到来之时水稻成熟,计划先由甲型收割机收割一部分,再由乙型收割机收割剩余部分,甲型收割机收割水稻每平方米的费用为0.3元,乙型收割机收割水稻每平方米的费用为0.5元,若要收割全部水稻的费用不超过5000元,问甲型收割机最少收割多少平方米的水稻?

查看答案和解析>>
科目:初中数学 来源: 题型:
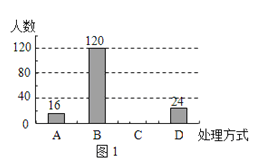
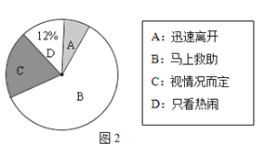
【题目】某校就“遇见路人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查,图1和图2是整理数据后绘制的两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)该校随机抽查了 名学生.
(2)将图1补充完整;
(3)在图2中,求“视情况而定”部分所占的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190﹣2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.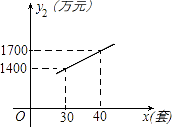
(1)直接写出y2(2)与x之间的函数关系式;
(2)求月产量x的取值范围;
(3)当月产量x(套)为多少时,这种产品的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com