
 如图,点O是原点,AB∥x轴,点M在线段AB上,且OM=2b,点E是线段AO的中点,若点B和点E关于直线OM对称,点B的坐标是(0,a),则点A的坐标是(3b,a) (结果用a,b表示).
如图,点O是原点,AB∥x轴,点M在线段AB上,且OM=2b,点E是线段AO的中点,若点B和点E关于直线OM对称,点B的坐标是(0,a),则点A的坐标是(3b,a) (结果用a,b表示). 分析 根据点B的坐标求出OB的长,再连接ME,根据轴对称的性质可得OB=OE,再求出AO的长度,然后利用三角函数得到∠A=30°,∠AOB=60°,进一步得到∠BOM=∠AOM=30°,再根据等角对等边得到AM=OM=2b,根据三角函数得到BM=$\frac{1}{2}$OM=b,从而求出AB的长,然后写出点A的坐标即可.
解答 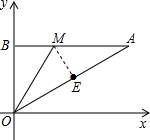 解:∵点B(0,a),
解:∵点B(0,a),
∴OB=a,
连接ME,
∵点B和点E关于直线OM对称,
∴OB=OE=a,
∵点E是线段AO的中点,
∴AO=2OE=2a,
∴∠A=30°,∠AOB=60°,
∴∠BOM=∠AOM=30°,
∴AM=OM=2b,
∵BM=$\frac{1}{2}$OM=b,
∴AB=BM+MA=3a,
∴点A的坐标是(3b,a).
故答案为:(3b,a).
点评 本题考查了轴对称的性质,坐标与图形性质,解直角三角形,熟练掌握轴对称的性质并作出辅助线构造出直角三角形是解题的关键.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
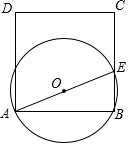 如图,正方形ABCD的边长为1,点E为BC边上一动点,以AE为直径作⊙O.
如图,正方形ABCD的边长为1,点E为BC边上一动点,以AE为直径作⊙O.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y是z的正比例函数 | B. | y是z的反比例函数 | ||
| C. | y是z的函数但不一定是反比例函数 | D. | y是z的函数但不一定是正比例函数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若∠A=20°,∠B=70°,则∠ACB的度数为 ( )
如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若∠A=20°,∠B=70°,则∠ACB的度数为 ( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.3008×106 | B. | 13.008×105 | C. | 1.3008×104 | D. | 0.13008×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1道 | B. | 2道 | C. | 3道 | D. | 4道 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
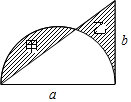 如图,已知直角三角形的两条直角边分别为a、b,以a为直径画一个半圆.若甲、乙两阴影部分的面积相等,则用a的代数式表示b=$\frac{1}{4}$πa.
如图,已知直角三角形的两条直角边分别为a、b,以a为直径画一个半圆.若甲、乙两阴影部分的面积相等,则用a的代数式表示b=$\frac{1}{4}$πa.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x+1)=64 | B. | x(x-1)=64 | C. | (1+x)2=64 | D. | (1+2x)=64 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com