
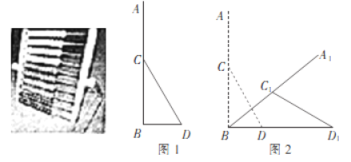
����Ŀ����ͼ��ʾ�����������һ������AB��һ��֧�ż�CD��ɣ������ʾ��ͼ��ͼ1��ʾ�����AB��BD��AB=40cm��CD=25cm����CΪAB���е㣮��Ϊ�˷����ͯ�������������ߵİڷţ���AB�Ƶ�B˳ʱ����ת��CD�Ƶ�C��ת��ͬʱ��D��ˮƽ����(��ͼ2)������C1��BD�ľ���Ϊ10cmʱֹͣ�˶������A������·���ij��͵�D�����ľ��룮(��������������ο����ݣ�![]() ��1��732��
��1��732�� ![]() ��4��583����3��142)
��4��583����3��142)
���𰸡�42cm��25cm
��������
�������ù��ɶ����ó�BD�ij����ٹ���C1��C1H��BD1�ڵ�H�������ó�BH=10![]() cm�������ABC1=60�������û�����ʽ�����A������·���ij��������D1C1=25cm��C1H=10cm�������ó�D1H��BD1�ij������ɵó��𰸣�
cm�������ABC1=60�������û�����ʽ�����A������·���ij��������D1C1=25cm��C1H=10cm�������ó�D1H��BD1�ij������ɵó��𰸣�
��AB=40����C��AB���е㣬
��BC=![]() AB=20cm��
AB=20cm��
��AB��BD��
���CBD=90����
��Rt��BCD��BC=20cm��DC=25cm��
��BD=![]() =
=![]() =15��cm����
=15��cm����
����C1��C1H��BD1�ڵ�H��
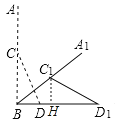
���C1HD=C1HD1=90����
��Rt��BC1H��BC1=20cm��C1H=10cm��
���C1BH=30������BH=10![]() cm��
cm��
���ABC1=60����
�ʵ�A������·���ij�Ϊ��![]() ��42��m����
��42��m����
��Rt��D1C1H��D1C1=25cm��C1H=10cm��
��D1H=![]() =
=![]() ��cm����
��cm����
��BD1=BH+HD1=10![]() +5
+5![]() ��17.32+22.915=40.235��cm����
��17.32+22.915=40.235��cm����
���D�����ľ���Ϊ��BD1-BD=40.235-15=25.235��25��cm����
�𣺵�D�����ľ���Ϊ25m����A������·���ij�Ϊ42m��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
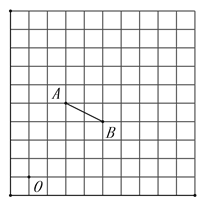
����Ŀ����ͼ�����ɱ߳�Ϊ1����λ���ȵ�С��������ɵ�10��10����������֪��O��A��B��Ϊ�����ߵĽ���.
��1���ڸ��������������Ե�OΪλ�����������߶�AB�Ŵ�Ϊԭ����2�����õ��߶�![]() ����A��B�Ķ�Ӧ��ֱ�Ϊ
����A��B�Ķ�Ӧ��ֱ�Ϊ![]() ��.�����߶�
��.�����߶�![]() ;
;
��2�����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת90���õ��߶�
��ʱ����ת90���õ��߶�![]() .�����߶�
.�����߶�![]() ;
;
��3����![]() Ϊ������ı���
Ϊ������ı���![]() ������� ��ƽ����λ.
������� ��ƽ����λ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
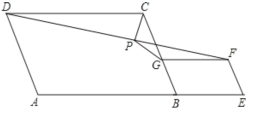
����Ŀ����ͼ,��ƽ���ı���ABCD��ƽ���ı���BEFG��,AB=AD,BG=BE,��A�� B�� E��ͬһֱ����,P���߶�DF���е�,����PG��PC������ABC=��BEF=60��,��![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
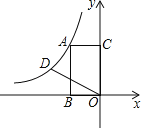
����Ŀ����ͼ������ABOC�Ķ���B��C�ֱ���x�ᣬy���ϣ�����A�ڵڶ����ޣ���B������Ϊ����2��0�������߶�OC�Ƶ�O��ʱ����ת60�����߶�OD��������������y=![]() ��k��0����ͼ��A��D���㣬��kֵΪ______��
��k��0����ͼ��A��D���㣬��kֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1��y��6x+6��x�ᡢy��ֱ���A��D���㣬ֱ��l2��y����x+3��x�ᡢy��ֱ���B��C���㣮
��1����ֱ��l2����һ��E��ʹ|AE��DE|��ֵ�����|AE��DE|�����ֵ��
��2����ABΪ��������ABMN����C�ڱ�MN�ϣ�����P��B������������BM�����ƶ�������PAB����ֱ��PA�ĶԳơ�PAB'���Ƿ���ڵ�P��ʹ�á�PMB'��ֱ�������Σ������ڣ���ֱ��д�����з�������ĵ�P�����ꣿ�������ڣ���˵�����ɣ�
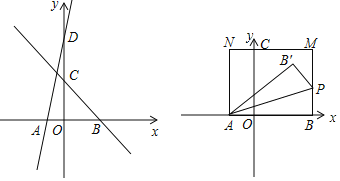
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶640��ѧ�����������Ӧ������ѵǰ������μ���һ��ˮƽ��ͬ�IJ��ԣ�����ͬһ���ֳ������ϸ��������ϸ�������������3���ȼ���Ϊ�˽���ѵЧ�����ó�������ķ�ʽ���г�ȡ32��ѧ����2�β��Եȼ��������Ƴ�����ͳ��ͼ��

��1����32��ѧ��������ѵ�����Եȼ������ϸ����İٷֱȱ���ѵǰ�����˶��٣�
��2�����Ƹ�У���꼶ѧ���У���ѵǰ����ȼ�Ϊ���ϸ���������������ѧ�����ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
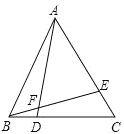
����Ŀ����ͼ����ABC�ǵȱ������Σ���D��E�ֱ���BC��AC�ϣ���BD��CE��AD��BE�ཻ�ڵ�F��
(1)֤������ABD�ա�BCE��
(2)֤������ABE�ס�FAE��
(3)��AF��7��DF��1����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2011�Ĵ����ݣ�23��6�֣��ڴ���װ��������ͬ��С�����ǵı�ŷֱ�Ϊ2��7���ҿڴ���װ��������ͬ��С�����ǵı�ŷֱ�Ϊ4��5�����ڴ���װ��������ͬ��С�����ǵı�ŷֱ�Ϊ3��8��9������3���ڴ��и������ȡ��1��С��
��1����ȡ����3��С��ı��ȫ�������ĸ����Ƕ��٣�
��2����ȡ��������С��ı�ŷֱ��ʾ�����߶εij��ȣ�����Щ�߶��ܹ��������εĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ�ӹ��������г����н�����Ըó�������һ����������Ʒ���δ����������۽���Ԥ�⣬����������ģ�ͣ����t���£�����Ʒ������ΪP����λ���䣩��P��t֮�������ͼ��ʾ������ϵ����ͼ�����߶�AB��������A�����߶�BC����ϣ����t��������ÿ���ë����ΪQ����Ԫ������Q��t�������¹�ϵQ=2t+8��0��t��24����
��1����P��t�ĺ�����ϵʽ��6��t��24����
��2���ó��ڵڼ������ܹ�������ë�������ë�����Ƕ��٣�
��3�������鷢�֣�����ë������40000�Ҳ�����43200Ԫʱ�����²�Ʒԭ���Ϲ������г������г����ʱ�������Ϊ����г��������ô����δ�������еڼ�����Ϊ��г�£�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com