
����Ŀ����ͼ��ֱ��l1��y��6x+6��x�ᡢy��ֱ���A��D���㣬ֱ��l2��y����x+3��x�ᡢy��ֱ���B��C���㣮
��1����ֱ��l2����һ��E��ʹ|AE��DE|��ֵ�����|AE��DE|�����ֵ��
��2����ABΪ��������ABMN����C�ڱ�MN�ϣ�����P��B������������BM�����ƶ�������PAB����ֱ��PA�ĶԳơ�PAB'���Ƿ���ڵ�P��ʹ�á�PMB'��ֱ�������Σ������ڣ���ֱ��д�����з�������ĵ�P�����ꣿ�������ڣ���˵�����ɣ�
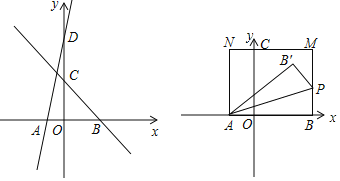
���𰸡���1��![]() ����2�����������ĵ�P������Ϊ��3��
����2�����������ĵ�P������Ϊ��3��![]() ����3��
����3��![]() ����
����
��������
��1����ͼ1�У�����D����ֱ��y����x+3�ĶԳƵ�D�䣬����CD�䣬AD�䣬�ӳ�AD�佻ֱ��BC��E����E��Ϊ����֤����DCD���ǵ���ֱ�������������D������꼴�ɽ�����⣮
��2�����������Σ���ͼ2��1�У�����PB��M��90��ʱ��A��B�䣬M���ߣ���ͼ2��2�У�����PMB�䣽90��ʱ����B������MN�ϣ��ֱ����ù��ɶ��������������ε�������⼴�ɣ�
�⣺��1����ֱ��l1��y��6x+6��x�ᡢy��ֱ���A��D���㣬ֱ��l2��y����x+3��x�ᡢy��ֱ���B��C���㣬
��A����1��0����D��0��6����B��3��0����C��0��3����
��ͼ1�У�����D����ֱ��y����x+3�ĶԳƵ�D�䣬����CD�䣬AD�䣬�ӳ�AD�佻ֱ��BC��E����E��Ϊ����
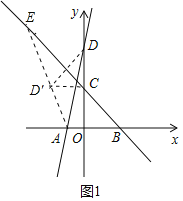
��OC��3��OD��6��
��CD��3��
�ߡ�DCE����OCB����ECD�䣽45�㣬
���DCD�䣽90�䣬
��D�䣨��3��3����
��AD�䣽![]() ��
��
��|AE��DE|�����ֵ��AD�䣽![]() ��
��
��2����ͼ2��1�У�����PB��M��90��ʱ��A��B�䣬M���ߣ�
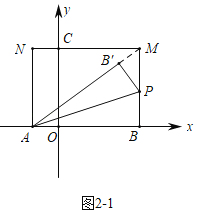
��Rt��ABM�У��ߡ�ABM��90�㣬AB��4��BM��3��
��AB��![]() ��
��
��AB��AB�䣽4��
��MB�䣽5��4��1����PB��PB�䣽x��
��Rt��PMB��������3��x��2��x2+12��
��ã�x��![]() ��
��
��P��3��![]() ����
����
��ͼ2��2�У�����PMB�䣽90��ʱ����B������MN�ϣ�
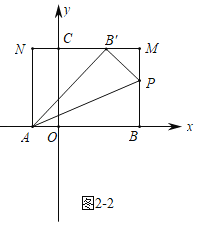
��Rt��ANB���У��ߡ�N��90�㣬AB�䣽AB��4��AN��3��
��NB�䣽![]() ��
��
�ߡ�AB��P����M����N��90�㣬
���NAB��+��AB��N��90�㣬��AB��N+��PB��M��90�㣬
���NAB�䣽��MB��P��
���ANB��ס�B��MP��
��![]() ��
��
��![]() ��
��
��PB�䣽![]() ��
��
��PB��PB�䣽![]() ��
��
��P��3��![]() ����
����
�������������������ĵ�P������Ϊ��3��![]() ����3��
����3��![]() ����
����


 �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д� Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2����2a+1��x+c��a��0����ͼ������ԭ��O��һ�κ���y��x��4��x�ᡢy��ֱ��ڵ�A��B��
��1��c���� ������A�������� ����
��2�������κ���y��a2����2a+1��x+c��ͼ����A����a��ֵ��
��3�������κ���y��a2����2a+1��x+c��ͼ�����AOBֻ��һ�������㣬ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
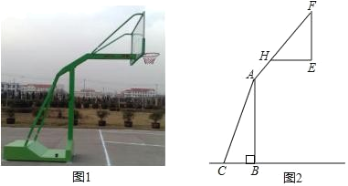
����Ŀ����ͼ1��2�ֱ���ij������ܵ�ʵ��ͼ��ʾ��ͼ����֪����BC�ij�Ϊ0.60m������BC��֧��AC���ɵĽǡ�ACB=75������A��H��F��ͬһ��ֱ���ϣ�֧��AH�εij�Ϊ1m��HF�εij�Ϊ1.50m������ײ�֧��HE�ij�Ϊ0.75m��
(1)������ײ�֧��HE��֧��AF���ɵĽǡ�FHE�Ķ�����
(2)�����嶥��F������ľ��룮(�����ȷ��0.1 m���ο����ݣ�cos75���0.2588��sin75���0.9659��tan75���3.732��![]() ��1.732��
��1.732��![]() ��1.414)
��1.414)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һԪ���η���ax2+bx+c��0 ������ x1��x2��Ϊ����������x1��x2��������1��x1��x2��2����ô��������������Ѻø�����
��1�����̣�x��![]() ����x��
����x��![]() ����0_____���Ѻø�������������������û��������
����0_____���Ѻø�������������������û��������
��2����֪����x�� x2����t��1��x+t��2��0�����Ѻø������� t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���ﴫͳ�Ļ���ijУ��չ�������о����Ļ����Ķ��������������Ϊ�˽��ߡ����꼶ѧ��(�ߡ����꼶����600��ѧ��)���Ķ�Ч������У�����˾����Ļ�֪ʶ�������ִ������꼶�������ȡ20��ѧ���ľ����ɼ�(�ٷ���)���з������������£�
�ռ����ݣ�
���꼶��79��85��73��80��75��76��87��70��75��94��75��79��81��71��75��80��86��59��83��77��
���꼶��92��74��87��82��72��81��94��83��77��83��80��81��71��81��72��77��82��80��70��41��
�������ݣ�
|
|
|
|
|
| |
���꼶 | 0 | 1 | 0 | a | 7 | 1 |
���꼶 | 1 | 0 | 0 | 7 | b | 2 |
�������ݣ�
ƽ���� | ���� | ��λ�� | |
���꼶 | 78 | 75 |
|
���꼶 | 78 |
| 80.5 |
Ӧ�����ݣ�
(1)���ϱ���գ�a= ��b= ��c= ��d= ��
(2)���Ƹ�У�ߡ��������꼶ѧ���ڱ��ξ����гɼ���90�����ϵĹ��ж����ˣ�
(3)����Ϊ�ĸ��꼶��ѧ���Ծ����Ļ�֪ʶ���յ�����ˮƽ�Ϻã���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
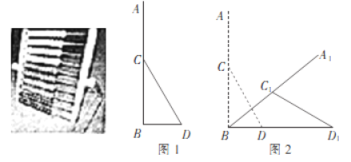
����Ŀ����ͼ��ʾ�����������һ������AB��һ��֧�ż�CD��ɣ������ʾ��ͼ��ͼ1��ʾ�����AB��BD��AB=40cm��CD=25cm����CΪAB���е㣮��Ϊ�˷����ͯ�������������ߵİڷţ���AB�Ƶ�B˳ʱ����ת��CD�Ƶ�C��ת��ͬʱ��D��ˮƽ����(��ͼ2)������C1��BD�ľ���Ϊ10cmʱֹͣ�˶������A������·���ij��͵�D�����ľ��룮(��������������ο����ݣ�![]() ��1��732��
��1��732�� ![]() ��4��583����3��142)
��4��583����3��142)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ھ���ABCD��,AB=4,BC=2,��E�DZ�BC���е�,PΪAB��һ��,����PE,����E��PE�Ĵ��߽�����AD�ڵ�Q,����PQ,��AP�ij�Ϊt.
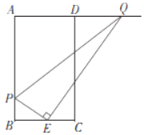
(1)�ú�t�Ĵ���ʽ��ʾAQ�ij�;
(2)����PEQ���������10,��t��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����C����O��һ�㣬����C��ֱ�߽�AB���ӳ����ڵ�D��AE��DC������ΪE��F��AE����O�Ľ��㣬ACƽ����BAE��

��1����֤��DE����O�����ߣ�
��2����AE=6����D=30������ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ͼ��ʾ����֪���κ���y��ax2+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C���Գ���Ϊֱ��x��1��ֱ��y����x+c��������y��ax2+bx+c����C��D���㣬D����x���·��Һ�����С��3�������н��ۣ���a��b+c��0����2a+b+c��0����x����x+b����a+b����a����1��������ȷ���У�������
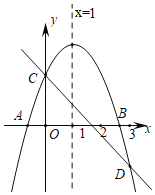
A.4��B.3��C.2��D.1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com