练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某课外学习小组有5人，在一次数学测验中的成绩分别是120、130、135、120、125，下列说法不正确的是（　　）
    A.众数是120
    B.方差是34
    C.中位数是135
    D.平均数是126

    【答案】C
    【解析】解：120出现了2次，最多，故众数为120，A正确；
    平均数为：（120+130+135+120+125）=126，D正确；
    方差为：×[2×（120﹣126）2+（130﹣126）2+（135﹣126）2+（125﹣126）2]=34，B正确；
    中位数为125，C错误．
    由于该题选择不正确的，故选C．
    【考点精析】利用算术平均数和中位数、众数对题目进行判断即可得到答案，需要熟知总数量÷总份数=平均数．解题关键是根据已知条件确定总数量以及与它相对应的总份数；中位数是唯一的，仅与数据的排列位置有关，它不能充分利用所有数据；众数可能一个，也可能多个，它一定是这组数据中的数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】先化简，再求值2x2﹣3x+7﹣4x2+3x+1，其中x＝﹣2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为缓解中低收入人群和新参加工作的大学生住房的需求，某市将新建保障住房3600000套，把3600000用科学记数法表示应是（ ）
    A.0.36×107
    B.3.6×106
    C.3.6×107
    D.36×105

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1+∠2=180°，∠B=∠3，你能判断∠C与∠AED的大小关系吗？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在△ABC中，∠BAC=90°，AB=AC，点E在AC上（且不与点A，C重合），在△ABC的外部作△CED，使∠CED=90°，DE=CE，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．

    （1）请直接写出线段AF，AE的数量关系 ；

    （2）将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请判断线段AF，AE的数量关系，并证明你的结论；

    （3）在图②的基础上，将△CED绕点C继续逆时针旋转，请判断（2）问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

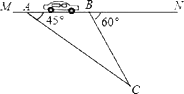
    【题目】“为了安全，请勿超速”．如图，一条公路建成通车，在某直线路段MN限速60千米/小时，为了检测车辆是否超速，在公路MN旁设立了观测点C，从观测点C测得一小车从点A到达点B行驶了5秒钟，已知∠CAN=45°，∠CBN=60°，BC=200米，此车超速了吗？请说明理由．

    （参考数据：≈1.41，≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果|m﹣3|+(n+2)2＝0，那么mn的值是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：x2+4x﹣5=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程m2x2+（4m﹣1）x+4=0的两个实数根互为倒数，那么m的值为（　　）
    A.2
    B.-2
    C.±2
    D.±

    查看答案和解析>>

    同步练习册答案